Downsample from 48khz to 8khz

I was tinkering. Wrote some code to low pass and downfilter a 48khz audio signal to only 8khz. Here’s some example output. It filters out audio above 2.7khz or so, and then downsamples to 8khz. The audio is just some test of Holst’s Mars, just meant to test.

#include <stdio.h>
#include <sndfile.h>

#define NTAPS   (55)
#define SKIP    6

float coef[55] = {
 1.06012E-04,  2.57396E-04,  4.39093E-04,  5.24290E-04,  3.41603E-04,
-2.52071E-04, -1.25563E-03, -2.42069E-03, -3.23354E-03, -3.03919E-03,
-1.31274E-03,  1.99613E-03,  6.19226E-03,  9.80711E-03,  1.09302E-02,
 7.88736E-03,  8.59963E-05, -1.12812E-02, -2.30159E-02, -3.04057E-02,
-2.84214E-02, -1.33337E-02,  1.57597E-02,  5.60551E-02,  1.01222E-01,
 1.42716E-01,  1.71912E-01,  1.82477E-01,  1.71912E-01,  1.42716E-01,
 1.01222E-01,  5.60551E-02,  1.57597E-02, -1.33337E-02, -2.84214E-02,
-3.04057E-02, -2.30159E-02, -1.12812E-02,  8.59963E-05,  7.88736E-03,
 1.09302E-02,  9.80711E-03,  6.19226E-03,  1.99613E-03, -1.31274E-03,
-3.03919E-03, -3.23354E-03, -2.42069E-03, -1.25563E-03, -2.52071E-04,
 3.41603E-04,  5.24290E-04,  4.39093E-04,  2.57396E-04,  1.06012E-04,
} ;

float input[NTAPS] ;

main()
{
    SNDFILE *inp, *out ;
    SF_INFO inpinfo ;
    SF_INFO outinfo ;
    int i, j ;
    float sum ;

    inp = sf_open("input.wav", SFM_READ, &inpinfo) ;

    outinfo.samplerate = 8000 ;
    outinfo.channels = 1 ;
    outinfo.format = SF_FORMAT_WAV | SF_FORMAT_PCM_16 ;
    out = sf_open("output.wav", SFM_WRITE, &outinfo) ;

    fprintf(stderr, "%d samples/second file, %d seconds\n", 
        inpinfo.samplerate,
        inpinfo.frames / inpinfo.samplerate) ;
    
    for (i=0; i+SKIP < inpinfo.frames; i += SKIP) {
        sf_read_float(inp, input+NTAPS-SKIP, SKIP) ;
        sum = 0.0 ;
        for (j=0; j<NTAPS; j++)
            sum += coef[j] * input[j] ;
        sf_write_float(out, &sum, 1) ;

        for (j=0; j+SKIP<NTAPS; j++)
            input[j] = input[j+SKIP] ;
    }
    sf_close(inp) ; sf_close(out) ;
}

Addendum: Alan wanted to know how I computed the filter coefficients. Excellent question! I used Ken Steiglitz’s METEOR program. Here’s the input file:

          55          55     smallest and largest length
c
left     direction of pushed specs
           2     number of specs pushed
           3           4     specs pushed
         500     number of grid points
limit spec
+     upper limit
arithmetic interpolation
not hugged spec
 0.00000E+00 5.62500E-02     band edges
 1.00100E+00 1.00100E+00     bounds
limit spec
-     lower limit
arithmetic interpolation
not hugged spec
 0.00000E+00 5.65200E-02     band edges
 9.99000E-01 9.99000E-01     bounds
limit spec
+     upper limit
arithmetic interpolation
not hugged spec
 2.50000E-01 5.00000E-01     band edges
 1.00000E-04 1.00000E-04     bounds
limit spec
-     lower limit
arithmetic interpolation
not hugged spec
 2.50000E-01 5.00000E-01     band edges
 0.00000E+00 0.00000E+00     bounds
end

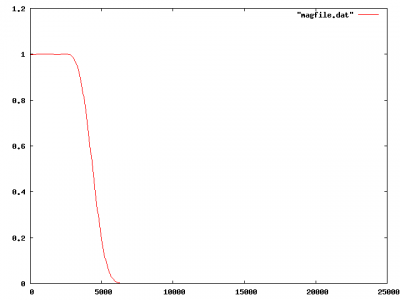
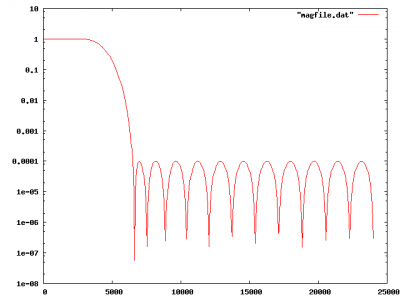
The file is a little odd, but basically i set up unity gain on the interval running from 0 to 0.05625 (which is 0 to 2.7khz at a sampling rate of 48khz), and then I set the response from .25 to .5 (12khz to 24kz) to less than -40db. I then set the filter length, and told the design program to “push” the edge of constraints 3 and 4 to the left. Here’s the resulting spectrum in linear scale and then log scale:

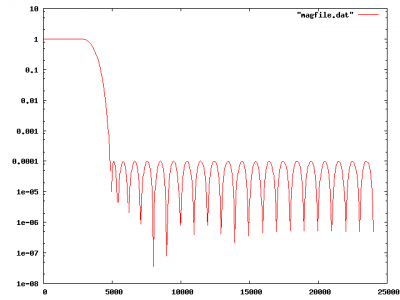
Staring at this now, I realize that this probably isn’t quite working the way I intended. I need to trim all freqs above 4khz to sample at 8khz. This still has significant frequency content at 5khz, which could result in significant aliasing. Increasing the size of the filter to length 95, I ended up with the following log response.