brainwagon

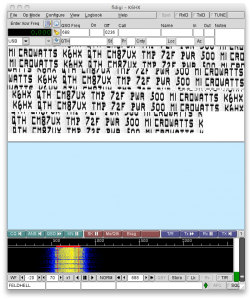
Update: Welcome Hack-a-day readers! If you are looking for the schematics for this “transmitter” (really just a simple oscillator, send some love to radio guru Steve Weber over at his website. You could really use any oscillator you like, even a canned oscillator (although the square waves would generate lots of harmonics). Yesterday’s project coupled [...]

Before toddling off to bed last night, I did a bit more tinkering, and a bit of thinking, and then a bit of research. The YouTube video I made showed that the spurious radiation from just attaching a clip lead from the oscillator to my oscilloscope gave enough signal to inject itself into my RFSpace [...]