Nothing too exciting going on, but minor bits of code and play have been done, so I thought I’d update.
First of all, there is a program for decoding SSTV on the Pi, called QSSTV. I don’t have a proper sound setup on the Pi yet, so I couldn’t test it live on the air, but I did take one of my pregenerated Martin 1 images and asked it to decode, which it did quite well:
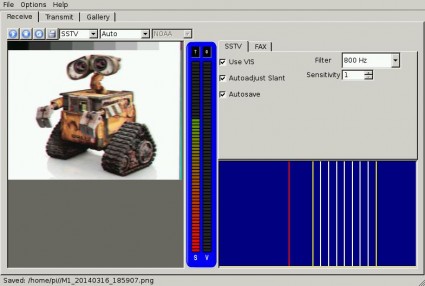
Not bad at all. While investigating qsstv’s capabilities, I discovered that the latest 8.x versions suppert digital SSTV. Well, except it isn’t built into the qsstv version (my guess is that the Pi doesn’t have quite enough oomph to do the necessary math in real time). But that’s pretty cool: I’ll have to check that out sometime soon.
But anyway…
I also coded up a Scotty 1 encoder, so now I have encoders for Martin 1, Scotty 1, Robot36 and Robot72 modes. I found this great book online which had many details about the different modes. It was quite helpful. It actually documents the modes a lot better than the ARRL Image Communications Handbook and is, well, free. Awesome.
One question I’ve been interested in for a while is “which mode is best?” Of course, we have to define what we mean by “best”. After all, Robot36 sends an image in half the time of Robot72, and about one quarter the time as Martin M1. My question was: how much better image can we expect from Martin, given that it takes 4x as long. Another question was “how much bandwidth does each mode use?” In the ARRL Image Communications Handbook, they have a formula which computes bandwidth but it didn’t make a great deal of sense to me.
I don’t know how to precisely answer either of these, but I thought I’d write some code to simply compute the power spectra of a bunch of some sample sstv recordings. So I did. It basically just loads the sound samples from the SSTV file, window it (I used the Blackman-Nutall window, for no real reason) runs an FFT (using the fftw3 library) and compute the power spectrum. It’s pretty easy. I then encoded a simple color bar image in three different modes, and graphed them all up using gnuplot.
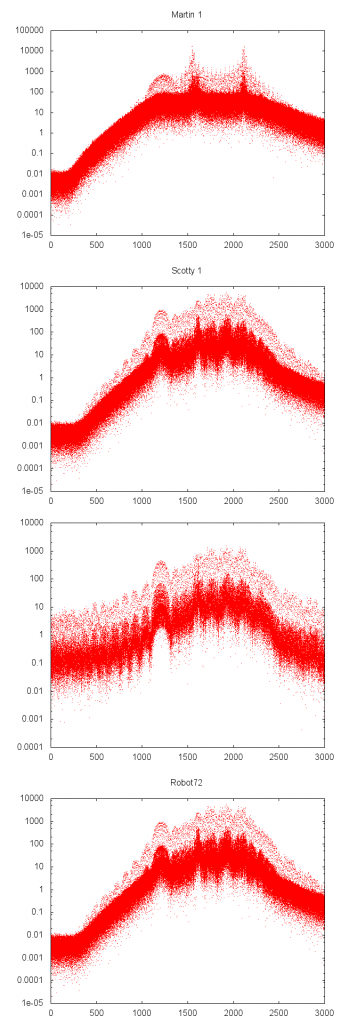
Staring at it, well, they don’t seem that different really. I should figure out the frequency bounds that (say) cover 85% of the total energy, but just eyeballing it, it doesn’t seem that bad.
I also did some minor tweaking to add in additive white Gaussian noise, but I haven’t gotten that entirely working so I could do an apple to apples comparison of how each modes does in total power at various levels of noise. And I’m looking for an HF path simulator too.
That’s about it for now. Stay tuned for more.