I suspect the world would be better if that percentage were even greater.
47 Some 28? mistakes in Gould’s The Game of Draughts
Earlier, I blogged about the historic book available from Google Books called Gould’s The Game of Draughts. While surveying a few problems, I noticed that my play was significantly different, and included a number of different outcomes for a couple of tested positions. So, I decided to use the newly added 8 piece Cake endgame database (thanks Martin, for releasing the code and the databases) and see if there were any mistakes I could find. Mind you: these are mistakes which the database points out Immediately, it doesn’t actually point out mistakes in play that require search. I found 47 errors, which for fun, I’ll list below.
I think I am going to (for fun) systematically work through these, and document the improved lines.
Addendum: I seem to have a bug in my code. The list wasn’t correct. I’ll replace it when I verify the results.
Addendum2: Here’s my list of 28 mistakes. I think it’s right, but it might not be, I’m still confused by some of the database issues.
916 : Gould’s Problems #30 is actually a loss for white
986 : Gould’s Problems #97 is actually a draw
1019 : Gould’s Problems #130 is actually a loss for red
1023 : Gould’s Problems #134 is actually a loss for red
1025 : Gould’s Problems #136 is actually a draw
1033 : Gould’s Problems #144 is actually a draw
1086 : Gould’s Problems #197 is actually a loss for red
1094 : Gould’s Problems #205 is actually a draw
1107 : Gould’s Problems #218 is actually a draw
1108 : Gould’s Problems #219 is actually a draw
1171 : Gould’s Problems #281 is actually a draw
1404 : Gould’s Problems #516 is actually a loss for white
1658 : Gould’s Problems #767 is actually a loss for red
1660 : Gould’s Problems #769 is actually a draw
1668 : Gould’s Problems #777 is actually a win for red
1677 : Gould’s Problems #786 is actually a loss for white
1679 : Gould’s Problems #788 is actually a draw
1694 : Gould’s Problems #803 is actually a loss for red
1770 : Gould’s Problems #879 is actually a draw
1774 : Gould’s Problems #883 is actually a draw
1775 : Gould’s Problems #884 is actually a loss for white
1817 : Gould’s Problems #924 is actually a loss for red
1821 : Gould’s Problems #928 is actually a win for red
1902 : Gould’s Problems #1009 is actually a loss for white
1923 : Gould’s Problems #1030 is actually a win for red
1930 : Gould’s Problems #1037 is actually a draw
1958 : Gould’s Problems #1065 is actually a loss for white
1972 : Gould’s Problems #1079 is actually a loss for white
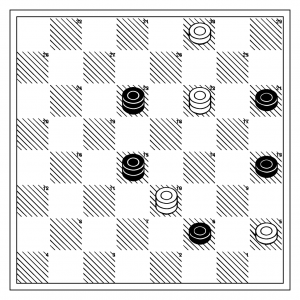
Addendum3: Check out this position from the list above with nine pieces:
The database code sees this as a draw, in spite of the fact that it only has up to eight pieces, because the capture resolution code removes one capture from the game before it does any database lookups.
From Gould's The Art of Draughts, problem #281
Comments
Comment from Mark
Time 10/17/2014 at 12:28 pm
Wow Jim. Thanks for your post! I drift in and out of working on my checkers program, and have been at your website many times, trying to learn more about checkers. I’ll double check Problem 30 and see where I went astray. I made some modification to Milhouse recently that has caused some instability in the db lookups.
Comment from Jim Loy
Time 6/5/2016 at 10:06 am
#97 is a big surprise, for a human solver. Here is the position, by T. Brown: [FEN “W:W22,21,K11:BK23,K3.”]. Here is the draw: 21-17 23-26* 11-15 26-23* 15-10 23-26* 10-6 3-8* 6-1 8-11 22-18 11-8*! (Brown shows 26-22? to a WW in H. Lyman’s Problem Book, later in J. Gould’s book) 17-13 26-22* 18-14 22-17* 14-10 8-11* 10-6 17-14 6-2 which is a drawn position by R. McCulloch in B. Boland’s Masterpieces p.152 note A at the top of the page, colors reversed. I typed these three books into my database, years ago, so now I can access all this info.
Comment from Jim Loy
Time 10/17/2014 at 10:15 am
Well done. Most of your corrections can be found in the appendix of Gould’s Problem Book (as it is often called). I have the 3rd edition. I don’t know which editions have this appendix, which is before the bridge endings. Most of the other corrections can be found in Jim Loy’s Checker Problems vol. 1. A reader of my book recently pointed out that Problem 108 has nothing to do with Solution 108. By the way, Problem 30 is a draw.