I really like programmpraxis.com. Today, they had an interesting little task, not so much for the program itself, but for what it reminded me of. But first, the task: basically to simulate a simple set of differential equations which model a predator prey relationship. It’s not that hard really, this just implements the model using a Runge-Kutta integrator.

Wolves And Rabbits « Programming Praxis.

#!/usr/bin/env python

# http://programmingpraxis.com/2009/12/01/wolves-and-rabbits/

def population(r, w, rg, wg, rd, wd):
    def dr(x, y):
        return rg * x - rd * x * y
    def dw(x, y):
        return wg * x * y - wd * x 
    while True:
        yield r, w
        rh = r + dr(r, w) / 2.
        wh = w + dw(w, r) / 2.
        r = r + dr(rh, wh)
        w = w + dw(wh, rh)


g = population(40, 15, 0.1, 0.005, 0.01, 0.1)

for x in range(201):
        r, w = g.next()
        print r, w 

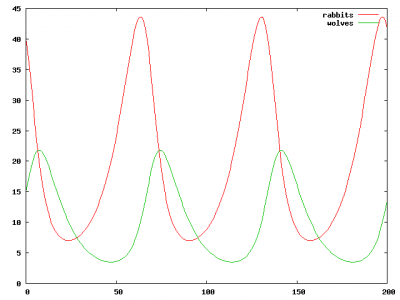
If you plot out the data, you get curves looking like this:

This reminded me of an article by A. K. Dewdeny from Scientific American back in December of 1984, entitled Shark and fish wage an ecological war on the toroidal planet Wa-Tor. Wator was an implementation of a shark/fish predator prey model, but displays a similar set of interleaved periodic population changes. Unlike this program though, it works by directly simulating the world by creating individual sharks and fish, and modeling their interactions. It was a fun, simple project which didn’t require any real understanding of mathematical methods.