I recall burning three or four weeks of a sabbatical getting Saccade.com on the air with Wordpress. So much tweaking…
Pictures of the Blum Blum Shub Random number generator…
A couple of years ago, I did a post about the Blum Blum Shub random number generator. I was watching Psych, and bored, so I decided to just make a picture of the random bits generated when I generated two 50 digit primes. Without further ado, or explanation, check it:
There do indeed seem to be very little pattern in it. Although if you knew the two primes that I used, you could generate the value of not just any bit here, but any bit in the future too.
Time for bed.
Comments
Comment from kiwimonster
Time 8/19/2010 at 10:50 am
I stared at it for a while, trying to make the words “April Fool” pop out of a random dot stereogram. Instead it looks more like the classic Japanese painting “Tsunami”. Perhaps a bit late in the year.
Comment from Jim Van Donsel
Time 8/23/2010 at 5:28 pm
Your primes are:
2983759823945837594304984948840598737485948749584730049721
and
8573059282710304384729394725029348271834083717394836494843
Right?
Comment from Mark VandeWettering
Time 8/24/2010 at 10:57 am
Uh, neither of those are primes. My own python implementation of Pollard rho factoring does trial divisions for primes < 1000, and then churns away to find the factorization of the first to be 3, 61, 151, 241, 164291, 789939529603967, and 3452320937986052799454668571981. The second is a bit easier, with factors 31, 28573, 10615249, 301424413, 4100243659 and 737734369141681373149593767. But I did discover a problem, both primes that I used should have been equivalent to 3 mod 4, and neither was.
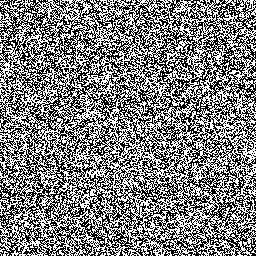
Comment from Pseudonym
Time 8/19/2010 at 12:13 am
Ah, but could one recreate the primes from that image alone?