Monthly Archives: October 2010

A 2010 “Graphical Computing” Calendar

The Make blog brought the Dead Reckonings blog to my attention. The blog is fascinating: consisting of essays of bits of lost mathematical lore, and nomography in particular. Author Ron Doerfler has some great stuff, and a cool give away: a calendar that demonstrates and explains many different kinds of nomographs. Of course, it’s kind of bad that I discovered the 2010 calendar in October of 2010, but such is life.

Dead Reckonings » A 2010 “Graphical Computing” Calendar.

Most Americans support an Internet kill switch

Sixty-one percent of Americans said the President should have the ability to shut down portions of the Internet in the event of a coordinated malicious cyber attack, according to research by Unisys.

Most Americans support an Internet kill switch.

51% percent would also like cars made out of candy that run on stupidity.

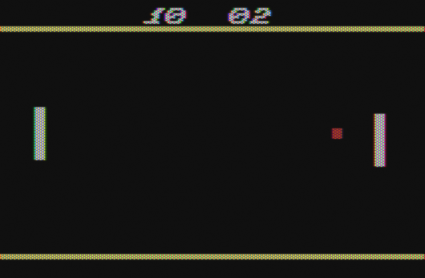
Ting-Tong? Pick-Pock? Keeping time on an Atari 2600…

Years ago, I remembered that someone (couldn’t remember who) had invented a clock which looked like a version of the classic video game “Pong”. A few minutes of searching now reveals who that was: Sander Mulder. I thought it was a cool idea, and I was thinking of a project that could get me back into programming the classic Atari 2600 again, so over the last three days, I hacked together my own version:

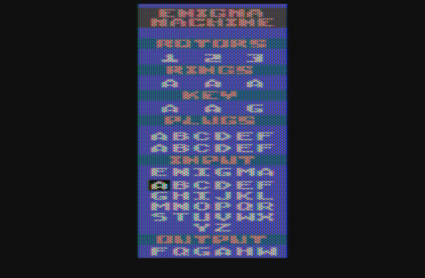
I did this using the same development environment that I used for my earlier magnum-opus, the Atari 2600 Enigma Machine

The assembler I used was an old version of P65, a 6502 assembler written in perl. It’s a tiny bit clunky, and doesn’t have any macro capability, but it does work. I have made use of the standard macro processor “m4” to make my source code a tiny bit tighter, and use the excellent Atari 2600 emulator Stella (available on Windows, Linux, or Mac OS X) to test and debug my program. The Atari clock fits rather nicely into 2K of ROM space, including a rather verbose splash screen.

I’ll probably write something up explaining why a grown man would work on writing any kind of software for a 30+ year old video game with only 128 bytes of memory, as soon as I can figure out something that doesn’t sound stupid.

Anyway, the clock seems to be working, and in simulation at least has kept rather excellent time (within one minute leaving it overnight) which isn’t bad at all. Once I get it burned into ROM, I’ll try to post the finished code and some pictures of the final clock.

Addendum: Here’s a short video showing the clock in action, filmed in truly crappy style with my iPhone.

httpv://www.youtube.com/watch?v=Q8_PfohAruc

Giants lead Phillies in the NLCS, 3-1

Wow, last night’s Game 4 of the NLCS was a real nailbighter, with the Giants ultimately prevailing 6-5 in a game which saw three different lead changes. I’ve begun to look at baseball-reference.com for play-by-play and statistical analysis, since it breaks down the outcome of each play and gives the change in winning percentage as results. The graphs of winning percentage seem to me a more natural (and more meaningful) statistic than “momentum” or other similar measures. They also identify the top plays (which are plays which significantly change the winning percentage). If you click through here, you can see the NLCS, and its up and down nature.

National League Championship Series (NLCS) Game 4, Phillies at Giants

If you compare this to the snoozer that was the Yankees defeating Texas 7-2, you can judge for yourself what the more interesting game was.

American League Championship Series (ALCS) Game 5, Rangers at Yankees

The Giants have the opportunity to close out the series tonight at home. I was at the Game 6 where the Giants closed out against St. Louis to earn their last trip to the big show. Sadly, I’ll have to watch this one at home, but I’m still pretty excited.

Lincecum vs. Halladay. It doesn’t get much better than that.

Bicycles & tricycles; an elementary treatise

Courtesy of the Make blog, here’s a link to an 1896 book on the design of bicycles and tricycles. I suspect a lot has been learned about bicycle design in the past 100 years, but I think it’s pretty interesting to see how much design theory had been developed at this early stage.

Bicycles & tricycles; an elementary treatise on their design and construction, with examples and tables : Sharp, Archibald, 1862-1934 : Free Download & Streaming : Internet Archive.

Why are baseball managers so stupid? Or is it just me?

Okay, I’m currently reading The Book: Playing the Percentages in Baseball because I hate to see intentional walks. Case in point: last night’s 7th inning walk of Chase Utley with one out and pitcher Roy Oswalt on second. You’d expect him to score on a double, but he’s not a huge immediate threat. In any case, they walked Utley, and Placido Polanco singles. Oswalt actually runs hard and scores, and you have two men on with one out, except now you are down a run, with Ryan Howard at bat. “Our situation has not improved.” During Howard’s at bat, the Phillies pull a double-steal. Howard strikes out, but now we have first base open, with Jayson Werth batting. Argh! Because of the double steal, they intentionally walk Werth to load the bases. Yes, Werth has been a hot hand in the playoffs, and Rollins was underachieving. But all those statistics are meaningless: it’s not like Rollins was really as bad as his recent slump would indicate. He’s a .272 career hitter (same as Werth), and if you give him plate appearances, he’ll show you it. He doubles, three runs scores, and it’s a sad day for the Giants.

Intentional walks really annoy me. Perhaps wrongly though. I was rereading some analysis of a game I remember from 2005.

Back in 2005, I blogged a tiny bit about the following game, which courtesy of baseball-reference.com, now has a very interesting analysis. In this game, the Astros were leading 4-2, and with the Cardinals batting in the bottom of the 9th, they got two quick outs, but Eckstein singles, and then steals second due to fielder indifference. “The theory” says at that point that the Cardinals only have a 4% chance of winning if the Cardinals played as an “average” team. Brad Lidge walks (on five pitches, not intentionally) Jim Edmonds, and St. Louis rises to a 7% win expectancy, again, assuming an “average team”. But the next batter isn’t an average batter: it’s Pujols. He cracks a home run, St. Louis scores three, and St. Louis wins (the Astros would win the series though).

October 17, 2005 National League Championship Series (NLCS) Game 5, Cardinals at Astros – Baseball-Reference.com.

So, here’s the question: on average teams, walking Edmonds only cost an additional 3% chance of handing the win to the opponents, but given that Pujols was the next batter, what’s a reasonable estimate for how costly that walk is? And if we did a similar analysis on the IBB’s in last night’s game, what would we find?

Well, you can go here and find out. The Giants only have a 1:4 chance of overcoming their deficit, and the intentional walk only changes that by a single percentage point. Polanco’s single increases that to 1:9, and the double steal increases that by 3%. Again, the intentional walk to Werth costs them about 1%, which frankly, I can’t argue with too much. The game is practically over, and these plays (as dramatic as they seem to me) hardly do much to harm SF’s small chance of making a comeback.

I hate it when I find out that my indignation is probably not righteous.

What do I know about baseball?

Back in 2004, I blogged a short message about the game four performance of the Red Sox against the Yankees.

brainwagon » Blog Archive » Red Sox 6, Yankees 4, 12 innings.

I had turned off the game after 7 innings, missing Bill Mueller’s RBI single in the bottom of the ninth to tie the game, and ultimately Ortiz’s game winning homer in the bottom of the 12th to win the game for Boston.

In my post, I warned the Red Sox that their defeat was inevitable.

Of course, this was 2004, where despite trailing the Yankees 3-0, the Red Sox rallied with four wins in a row in some of the most thrilling post season baseball I can remember, and ultimately going on to win the World Series.

I apparently don’t know much about baseball. “Inevitable doom” indeed.

How a geek tells his wife he loves her: an exercise in Python programming

I’m away from my better half this weekend, visiting my Mom and brother. I scheduled this a few weeks ago, but shortly after Carmen was granted an entry into the Nike Women’s Half Marathon on the same weekend. Rescheduling the visit with Mom would have been hard, so I decided to go anyway, and missed the opportunity to cheer her on.

But I’m a geek. On Saturday night, I hit upon a brilliant, romantic idea (or what passes for one when you are a geek). I knew I was gonna be busy during her run, so I decided to write a script that would text her ever half an hour with an encouraging message. That way, even if I got busy, she’d know I was thinking about her.

It probably would have helped had I started before 10:00pm on Saturday.

First of all, it’s pretty straightforward to send texts to someone using email. If you send an email to phonenumber@txt.att.net, the contents will get routed to the person. And using Python’s smtplib, sending email is pretty easy. Here’s a function that worked for me:

[sourcecode lang=”python”]

def emailtxt(addr, msg):
server = smtplib.SMTP("smtp.gmail.com", 587)
server.ehlo()
server.starttls()
server.ehlo()
server.login("myaccount@gmail.com", "mypassword")
server.sendmail("myaccount@gmail.com", addr, msg)
server.close()
[/sourcecode]

I decided to use my gmail account, but you can use whatever SMTP mail server you like.

So, now that I had a function to txt her, how to handle the scheduling? It turns out that Python has an interesting library called sched which can be used to implement a scheduler. Here’s the interesting bits:

[sourcecode lang=”python”]
import sched
import time

scheduler = sched.scheduler(time.time, time.sleep)

def timefor(t):
tp = time.strptime(t, "%a %b %d %H:%M:%S %Z %Y")
return time.mktime(tp)

scheduler.enterabs(timefor("Sun Oct 17 04:00:00 PDT 2010"), 1, sendit, (0,))
scheduler.enterabs(timefor("Sun Oct 17 04:30:00 PDT 2010"), 1, sendit, (1,))
scheduler.enterabs(timefor("Sun Oct 17 05:00:00 PDT 2010"), 1, sendit, (2,))
scheduler.enterabs(timefor("Sun Oct 17 05:30:00 PDT 2010"), 1, sendit, (3,))
scheduler.enterabs(timefor("Sun Oct 17 06:00:00 PDT 2010"), 1, sendit, (4,))
scheduler.enterabs(timefor("Sun Oct 17 06:30:00 PDT 2010"), 1, sendit, (5,))
…
scheduler.run()
[/sourcecode]

So, what does this do? It creates a scheduler object, which operates in real time (the time.time and time.delay functions are abstract functions that implement a time and delay function). It then uses the utility function timefor to figure out the absolute time when I wanted the event to occur, and when that time expires, it will call sendit, passing it the args in parens (which in my case is a message number in a table of nice things to send her, which I’ve omitted since they are too precious for words). When the run() method is called, the scheduler will wait until the appropriate time, and then make the calls.

I had it set to start sending messages at 4:00AM, since that is when she was going to wake up. Sadly, I screwed up the code slightly, and she didn’t get her first message until 7:30 or so. But she was successfully encourage every 30 minutes after that.

I’m very proud of her and her half-marathon performance. Neither of us are natural athletes, but she’s a constant inspiration to me, and makes me want to be stronger and better.

It’s too bad I’m such a geek.

Design of a simple ALU…

A couple of weeks ago, I noticed a bunch of links to a 16 bit ALU designed to operate using blocks which are defined in the game Minecraft. It got me thinking, and ordered the book that inspired that work. It contains the specification for an ALU which is very simple, and yet surprisingly powerful ALU (at least, considering the number of gates that it would take to implement it).

Here’s a C function that implements the ALU. I went ahead and just used the integer type, rather than the 16 bits specified in the Hack computer, but it doesn’t really matter what the word size is.

[sourcecode lang=”C”]
#define ZERO_X (1<<0)
#define COMP_X (1<<1)
#define ZERO_Y (1<<2)
#define COMP_Y (1<<3)
#define OP_ADD (1<<4)
#define COMP_O (1<<5)

unsigned int
alu(unsigned int x, unsigned int y, int flags)
{
unsigned int o ;

if (flags & ZERO_X) x = 0 ;
if (flags & ZERO_Y) y = 0 ;
if (flags & COMP_X) x = ~x ;
if (flags & COMP_Y) y = ~y ;
if (flags & OP_ADD)
o = x + y ;
else
o = x & y ;
if (flags & COMP_O) o = ~o ;
return o ;
}
[/sourcecode]

The function takes in two operands (x and y) and a series of six bit flags. The ZERO_X and ZERO_Y say that the X input and Z input should be set to zero. The COMP_X, COMP_Y, and COMP_O flags say that the X, Y, and output values should be bitwise negated (all the zeros become ones, and the ones zeros). The OP_ADD flag chooses one of two functions: when set, it means that the two operands should be added, otherwise, the two operands are combined with bitwise AND.

There are a surprisingly large number of interesting functions that can be calculated from this simple ALU. Well, perhaps not surprising to the hardware engineers out there, but I’ve never really thought about it. It’s obvious that you can compute functions like AND and ADD. Let’s write some defines:

[sourcecode lang=”C”]
#define AND(x,y) alu(x, y, 0)
#define ADD(x,y) alu(x, y, OP_ADD)
[/sourcecode]

You can also compute functions like OR using DeMorgan’s Law: OR(x,y) = ~(~X AND ~Y).

[sourcecode lang=”C”]
#define OR(x,y) alu(x, y, COMP_X|COMP_Y|COMP_O)
[/sourcecode]

You can make some constants such as zero and one. Zero is particularly easy, but one requires an interesting trick using twos-complement arithmetic.

To make sense of the definition of ONE, you need to know that in twos-complement arithmetic, -x = ~x + 1, or in other words, -x – 1 = ~x. Look at the definition of ONE, it computes ~(~0 + ~0). After the addition, the register contains all 1s, except for the low order bit. Negating that builds a one. You can also build a -1, or even a -2.

You can also obviously get either operand, or their logical complements. There are even multiple implementations:

We saw how we could add, we could also construct a subtractor:

[sourcecode lang=”C”]
#define SUB(x,y) alu(x, y, COMP_X|OP_ADD|COMP_O)
[/sourcecode]

We saw how we could compute +1 and -1, but we can also add these constants to X or Y..

I thought it was pretty neat or such a small implementation. The hardest part to implement is the adder, all the rest is a pretty trivial number of gates. If you use a simple ripple adder, even the adder is pretty small.

Addendum: Here’s a more (but not entirely) exhaustive list of functions that are implemented.

V4L2VD Home Page

I think I heard mention of this project during a recent episode of the FLOSS podcast a couple of weeks ago, and thought that it was an interesting idea, so remembered to track it down this morning. The basic idea is to provide a “loopback” device for video. You could write a program which can send out video frames, which are then read by any device that can read from v4l2 devices (like mplayer or mencoder). I have a couple of ideas for how this could be fun.

Sadly, typing “make” didn’t have the desired effect on my “Jaunty Jackalope” machine, and looking back, it seems that it hasn’t had an update since March 2008. It’s probably a fairly minor thing. I’ll try to work out the details later, and see if I can get it going.

V4L2VD Home Page

Addendum: Some more playing around yielded some new links of interest. The v4l2vd project mentioned the older vloopback, which is mostly unsupported, but which is apparently tagging along with the motion project, which does software motion detection on webcams (and notably v4l devices). You can find the software and such here, including a test application which accepts video from one device, and writes it back out to another.

I got onto this stuff by looking at the flashcam project, which I found while trying to find something like ustream that could run on Linux.

Progress in number theory in the years 1998-2009

Dan Piponi passed along the following link to a nice paper summarizing the major results in number theory of the last decade or so. It’s mostly over my head (Dan is substantially smarter than I) but pretty interesting nonetheless. [1010.2484] Progress in number theory in the years 1998-2009.

On random numbers…

While hacking a small program today, I encountered something that I hadn’t seen in a while, so I thought I’d blog it:

My random number generator failed me!

I was implementing a little test program to generate some random terrain. The idea was pretty simple: initialize a square array to be all zero height. Set your position to be the middle of the array, then iterate by dropping a block in the current square, then moving to a randomly chosen neighbor. Keep doing this until you place as many blocks asu like (if you wander off the edge, I wrapped around to the other side), and you are mostly done (well, you can do some post processing/erosion/filtering).

When I ran my program, it generated some nice looking islands, but as I kept iterating more and more, it kept making the existing peaks higher and higher, but never wandered away from where it began, leaving many gaps with no blocks at all. This isn’t supposed to happen in random walks: in the limit, the random walk should visit each square on the infinite grid (!) infinitely often (at least for grids of dimension two or less).

A moment’s clear thought suggeseted what the problem was. I was picking one of the four directions to go in the least complicated way imaginable:

[sourcecode lang=”C”]
dir = lrand48() & 3 ;
[/sourcecode]

In other words, I extracted just the lowest bits of the lrand48() call, and used them as an index into the four directions. But it dawned on me that the low order bits of the lrand48() all aren’t really all that random. It’s not really hard to see why in retrospect: lrand48() and the like use a linear congruential generator, and they have notoriously bad performance in their low bits. Had I used the higher bits, I probably would never have noticed, but instead I just shifted to using the Mersenne Twister code that I had lying around. And, it works much better, the blocks nicely stack up over the entire 512² array, into pleasing piles.

Here’s one of my new test scenes:

Much better.

Nano-Satellite Launch Challenge

Apparently NASA is sponsoring the development of nanosatellite launch capabilities by sponsoring a two million dollar prize purse for the first team to launch a standard 1U Cubesat into orbit (payloads must complete at least one orbit) twice in a week.

NASA – Nano-Satellite Launch Challenge.

I found out about this by reading the Team Phoenicia blog, which announced an upcoming seminar on the Nanosatellite Launcher Challenge in cooperation with the Menlo Park Techshop. I’d love to attend, but sadly I’ve got another cool event booked for that weekend.

Draft Agenda for the Team Phoenicia/Techshop Nanosatellite Launcher Seminar

Another nifty balloon project…

Luke Gesissbuhler did a balloon launch, lofting an HD video camera and an Apple iPhone to lofty heights before recovering them. Very nice. The footage right after burst was kind of cool: I was wondering whether the fragments of the balloon or parachute tangled with the camera: perhaps dangling the camera on a longer tether could reduce the possibility of them tangling. Still, it all worked out in the end (and rather brilliantly!).

Inspirational.

Homemade Spacecraft from Luke Geissbuhler on Vimeo.