I’ve been taking a puppet making class, and I must admit, it’s been a lot of fun. Too much fun, in fact. I’ve been thinking about puppet making, watching puppet making videos, and scouring the web for inspiration and guidance.
To date, I’ve only completed one puppet (his name is Gerfil, and he may still acquire eyes), so I have a lot to learn, but it’s fascinating.
Gerfil is a pretty ordinary hand puppet, but has a shape which is more refined than many of the simple arts and crafts patterns you can see on line. But I got fascinated by the process of pattern making. Digging around, I discovered this nifty video.
I rather liked the spherical head, but thought that it was a little odd that he disassembled a baseball cap to generate the pattern. The mathematician in me thought that it must be possible to generate a similar pattern using, well, mathematics. I began by considering a couple of basic design criteria. The top of the head would be a hemisphere, divided into six identical gussets. I decided to settle on an eight inch diameter head, which means that the total circumference is about 25 1/8 inches around. Since all six gussets are identical, it makes the base of each triangular gusset a little over 4 inches across the base. I set the height to be the circumference divided by four, or a little over six inches. But then the question became how to draw the curve connecting the base to the apex of this triangle.
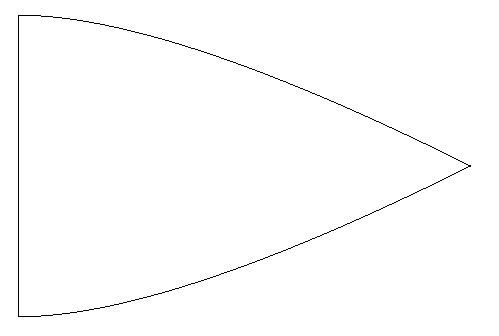
I decided to test a few ideas, and then print them out on paper to see how well they worked. I suspect that the ideas I used to generate this pattern are simply not quite right, but they aren’t hugely off. The sides are defined by a simple quadratic bezier, set to establish the tangent at the base to be a right angle, and the apex of the triangle to have a sixty degree angle.
The result looked like:
Cutting them out, and taping them together resulted in this:
It’s not bad, but it’s not great either. I suspect that if it was rendered in foam, it would be a bit better, as the foam is both compressible and stretchable. I suspect that to really do the job right, I’d need to simulate that more directly, and use real optimization techniques. But I did this while watching the Oscars (I’ve got 11 right so far) which means I can’t concentrate enough to pull off harder math. I’ll think about it more and try again in the next few days.
Addendum: Here’s a nice puppet pattern with some construction tips.