Lately, my lunch hours have been spent working on the NYT Crossword with my lunch companion Tom. While I find that the Thursday crosswords are often beyond my ability to do in the allotted time, between the two of us, more often than not we manage to plow through them. Slowly over time, we’ve begun to solve them slightly quicker, so I’ve branched out to doing the KenKen puzzles.

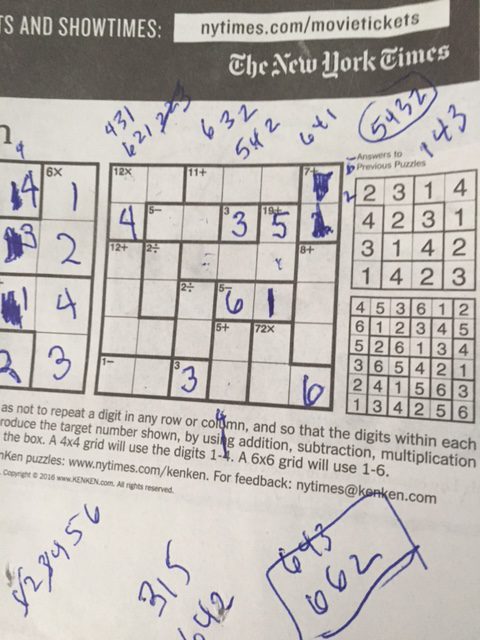
For those of you who haven’t seen these before, you can learn about them on their official website here. The 4×4 ones are usually pretty easy, but the last couple days have done some 6×6 puzzles have been shockingly hard. So much so, that today I got to this state on today’s puzzle:

Yes, I was using pen. And I made a mistake, although I can’t see what I was thinking when I did. And because I made a mistake, I couldn’t spot it, and I was hung up. The “4” in first column was wrong. I knew it could not be a 6 or 1, or a 3, or a 4, but for some reason I thought that the final column couldn’t be 4 and 3, but..

Never mind, it doesn’t matter what the mistake was.

By the end up twenty minutes I was annoyed, knew I had made a mistake, but decided to give into the urge to write a program to solve it. How long could it take?

Well, the answer was about 27 minutes.

This program doesn’t have any interface or flexibility, everything is hard coded. Basically it uses backtracking and fills in each square in order from bottom left to top right, and as the top most, right most square of each outlined area is finished, it checks to make sure that the sums/differences/whatever for the filled in region sum to the right values. I didn’t know how I was going to encode those constraints, so I just ended up writing a function that computes the proper constraint. This is not really the right way to do it: it’s error prone and requires recompilation of the code to change the puzzle. But it does work fairly well, once you type the expressions in correctly.

Once I got those straightened out, it blats out the solution in less than 1 millisecond on my desktop.

+---+---+---+---+---+---+
| 6 | 1 | 5 | 2 | 4 | 3 |
+---+---+---+---+---+---+
| 2 | 6 | 1 | 3 | 5 | 4 |
+---+---+---+---+---+---+
| 1 | 4 | 6 | 5 | 3 | 2 |
+---+---+---+---+---+---+
| 3 | 2 | 4 | 6 | 1 | 5 |
+---+---+---+---+---+---+
| 5 | 3 | 2 | 4 | 6 | 1 |
+---+---+---+---+---+---+
| 4 | 5 | 3 | 1 | 2 | 6 |
+---+---+---+---+---+---+

1 solutions found

It points out that the 4 should have been a 2 (IDIOT!) and then it all works out.

The code is 178 lines long, but is not particularly pretty/short/adaptable. Some day, I’ll have to tidy it up and make a better version.

But in case people find this stuff interesting, here it is. Remember: 27 minutes to write.

[sourcecode lang=”cpp”]
include <stdio.h>
#include <stdlib.h>
#include <string.h>

/*
* kenken.c
*
* A program inspired by a particular tough 6×6 puzzle that appeared
* on Thursday, May 11, 2016, which Tom Duff and I could not appear to
* get the answer to during our lunch hour. I thought that it was possible
* that I could write a program to solve the puzzle in less than an hour.
*
* Hence, this code.
*
*/

int total = 0 ;

#define DIM (6)

typedef struct t_puzzle_state {
int sq[DIM][DIM] ;
int r[DIM] ; // bitflag for values left in rows…
int c[DIM] ; // bitflag for values available in columns
} PuzzleState ;

void
PrintPuzzleState(PuzzleState *p)
{
int i, j ;

printf("+") ;
for(j=0; j<DIM; j++)
printf("—+") ;
printf("\n") ;

for (i=0; i<DIM; i++) {
printf("|") ;
for (j=0; j<DIM; j++) {

if (p->sq[DIM-1-i][j])
printf(" %1d |", p->sq[DIM-1-i][j]) ;
else
printf(" |") ;
}
printf("\n+") ;
for(j=0; j<DIM; j++)
printf("—+") ;
printf("\n") ;
}
printf("\n") ;
}

void
InitializePuzzleState(PuzzleState *p)
{
int i, j ;

memset((void *) p, 0, sizeof(*p)) ;

for (i=0; i<DIM; i++) {
for (j=1; j<=DIM; j++) {
p->r[i] |= (1<<j) ;
p->c[i] |= (1<<j) ;
}
}
}

void
HardcodePuzzleState(PuzzleState *p, int r, int c, int val)
{
p->sq[r][c] = val ;
p->r[r] &= ~(1<<val) ;
p->c[c] &= ~(1<<val) ;
}

#define SQUARE(i, j) ((i)*DIM+(j))
#define ABS(x) ((x)<0?(-(x)):(x))

int
ConstraintSatisfied(PuzzleState *p, int i, int j)
{
switch (SQUARE(i,j)) {
case SQUARE(0,1):
return ABS(p->sq[0][0] – p->sq[0][1]) == 1 ;
case SQUARE(0,2):
return p->sq[0][2] == 3 ;
case SQUARE(1, 3):
return (p->sq[0][3]+p->sq[1][3]) == 5 ;
case SQUARE(1, 4):
return (p->sq[0][4] * p->sq[0][5] * p->sq[1][4]) == 72 ;
case SQUARE(2, 2):
if (p->sq[2][2] == 2 * p->sq[1][2])
return 1 ;
if (p->sq[1][2] == 2 * p->sq[2][2])
return 1 ;
return 0 ;
case SQUARE(2, 4):
return ABS(p->sq[2][4] – p->sq[2][3]) == 5 ;
case SQUARE(3, 1):
if (p->sq[3][1] == 2 * p->sq[2][1])
return 1 ;
if (p->sq[2][1] == 2 * p->sq[3][1])
return 1 ;
return 0 ;
case SQUARE(3, 5):
return (p->sq[3][5]+p->sq[2][5]+p->sq[1][5]) == 8 ;
case SQUARE(4, 2):
return ABS(p->sq[4][2] – p->sq[4][1]) == 5 ;
case SQUARE(4, 3):
return p->sq[4][3] == 3 ;
case SQUARE(4, 4):
return (p->sq[4][4]+p->sq[3][2]+p->sq[3][3]+p->sq[3][4]) == 19 ;
case SQUARE(5, 1):
return (p->sq[4][0]*p->sq[5][0]*p->sq[5][1]) == 12 ;
case SQUARE(5, 4):
return (p->sq[5][2]+p->sq[5][3]+p->sq[5][4]) == 11 ;
case SQUARE(5, 5):
return (p->sq[5][5]+p->sq[4][5]) == 7 ;
default:
return 1 ;
}

return 1 ;
}

void
SolvePuzzleState(PuzzleState *p, int i, int j)
{
int v ;

if (i >= DIM) {
PrintPuzzleState(p) ;
total ++ ;
return ;
}

int pval = p->r[i] & p->c[j] ;

for (v=1; v<=DIM; v++) {
if ((pval & (1<<v)) == 0)
continue ;
// Try to place v in sq[i][j] ;
p->sq[i][j] = v ;

if (ConstraintSatisfied(p, i, j)) {
p->r[i] &= ~(1<<v) ;
p->c[j] &= ~(1<<v) ;

int ni, nj ;
nj = j + 1 ;
if (nj < DIM) {
ni = i ;
} else {
ni = i + 1 ;
nj = 0 ;
}

SolvePuzzleState(p, ni, nj) ;

p->r[i] |= (1<<v) ;
p->c[j] |= (1<<v) ;
}
}
p->sq[i][j] = 0 ;
}

main()
{
PuzzleState p ;
InitializePuzzleState(&p) ;
// HardcodePuzzleState(&p, 0, 2, 3) ;
// HardcodePuzzleState(&p, 4, 3, 3) ;

SolvePuzzleState(&p, 0, 0) ;
fprintf(stderr, "%d solutions found\n", total) ;
}
[/sourcecode]