brainwagon

Warning, spoilers ahead for those who are still interested in doing the problems themselves.

Part 1 of Day 19 was pretty simple, really. You could go ahead and read the specification yourself, but basically you have a relatively large number of text patterns which consist of jumbles of a relatively small number of characters (examples include “gwugr” and “rgw”) and you need to find which of a longer sequence (like “guuggwbugbrrwgwgrwuburuggwwguwbgrrbbguugrbgwugu”) can be constructed out of repetitions of some combination of these patterns. In the context of the problems, the long sequences are “towels” (read the problem description) and consist of any number of “stripe patterns” (hereafter referred to as patterns). Some towels will not be constructable out of the given stripe patterns. Part1 was to simply determine which could, and which could not.

It’s the kind of problem that is not particularly well suited for humans, but which has been studied extensively for decades. The theoretical framework is called “regular expressions” or “Discrete Finite Automata”. When I took a compiler class back in the mid 1980s, we wrote our own lexical analyzer generator that used techniques which were (from memory) well described in the classic text Compilers: Principles, Techniques and Tools by Aho, Sethi and Ullman, aka “the Dragon Book”. I still have my copy.

Anyway, regular expressions. Python (my chosen dagger which I use to approach all the Advent of Code problems) of course has a well developed regular expression library, which I thought might be a clever way to solve Part 1. In less than 12 minutes, I had this code:

#!/usr/bin/env python

import re

# data was in the format of a big chunk of small patterns,
# followed by list of towels we need to construct.

data = open("input.txt").read()

# find the patterns, and build a regular expression

patterns, towels = data.split("\n\n")
patterns = patterns.split(", ")

# "any number of any of the patterns, consuming the entire string."
regex = '^(' + '|'.join(patterns) + ')+$'

print(regex)

h = re.compile(regex)

c = 0
for design in towels.rstrip().split("\n"):
    if h.match(design):
        c += 1

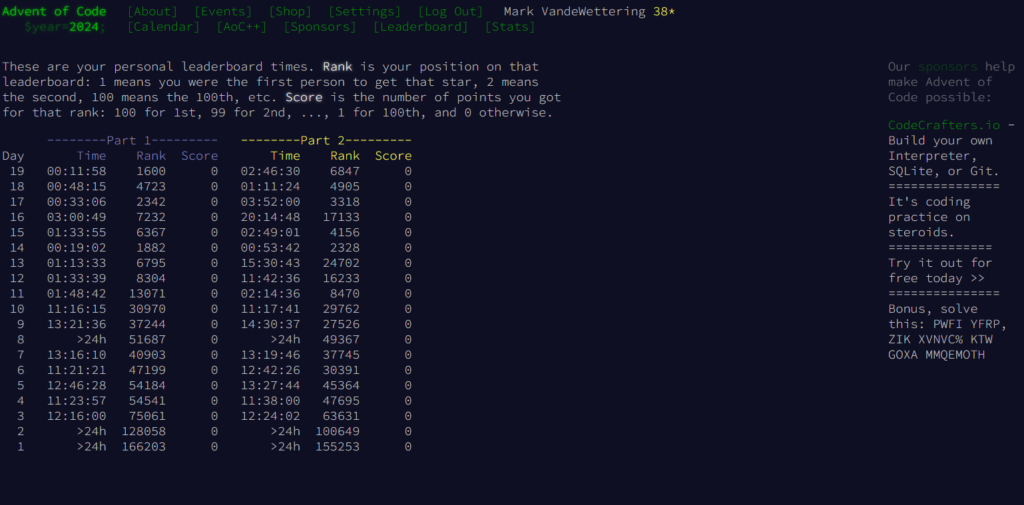
print(c, "designs are possible")

It’s simple, and it works. Because it leverages the “re” standard library, it might be expected to run quickly, and it does. On my cheap HP desktop I got from Costco, 18ms is enough to process all the input data and give the correct answer. I made one minor mistake, forgetting to add the caret at the beginning of the regex and the dollar sign at the end to make sure the entire string, but twelve minutes in and I had completed Part 1. Not the fastest (I was the 1600th to complete this phase of the puzzle, which isn’t bad by my standards) but I thought credible.

And here’s where I think I went wrong. In part 2, we are asked to determine the number of possible ways that each towel could be constructed, and add them up. My code in Part 1 was pretty useless for figuring that out. And because I am a smart guy with tons of experience and I’ve read the Dragon Book and the like, as well as Russ Cox’s excellent summary of the theory of fast pattern matching and perhaps it was the late hour (back in graduate school I made a rule not to write code after 10 pm, because my code would always seem stupid the next morning when I had coffee) but I embarked upon a complex, pointless, meandering exploration where I tried to recall how maybe I could use the same sort of techniques that I used oh-so-many years ago to solve this efficiently. I’ll outline basic notion, to tell you just how deep in the weeds I was. I didn’t get this to work, but I do think it is “sound” and could have been made to complete the second path.

Basically, the notion is to use a discrete finite automata to do the heavy lifting. (I’m doing this from memory, so please be patient if I don’t use the right or most precise terminology). Basically, we are going to generate a state machine that does all the heavy lifting. To make it somewhat simpler, let’s look at the basic example from original problem description:

r, wr, b, g, bwu, rb, gb, br

brwrr
bggr
gbbr
rrbgbr
ubwu
bwurrg
brgr
bbrgwb

When we begin, we are in “state 0”, or the start state. We will transition to other states by reading a character from the input, and then transitioning to different states (as yet undetermined). If we end up in the end state, and there is no more input to be processed, then we match, otherwise, we don’t and return failure.

We can build our transition table by looking at the “first” and “follow” sets (I didn’t have the Dragon book in front of me, but here is the idea):

At the start of input we are in State 0. If we look at the first character of any of the patterns, we see that they can be ‘r’, ‘w’, ‘g’, ‘b’. If we see a ‘u’, then we have no match, and would go to a “fail state”, and return zero.

But let’s say we are processing the input “brgr”. We are in State 0 or S0, looking at a character “b”. Let’s create the state S1. S1 would be “transitioned from the start state, and saw a b”. What are the possible patterns that we could still be in? We could have matched “b” pattern, and be back in a state where all the possible patterns are possible. Or, we could be in the “bwu” pattern, having read the b. Or we could be in the “br” pattern. Let’s say that S1 means “we could have just completed the “b” pattern, or we could be in the “bwu” pattern, or we could be in the “br” pattern”.

Now, what transitions happen after S1. Well, we create a new state for each of the possibilities. If we completed the B pattern, we are back into a state which looks identical to S0, we we may as well use it. If we read a w, we know we can only be in the state where the “bwu” is active. Let’s ignore that for now. If we read an “r”, we could have matched the “r” pattern. Or we could have completed the “br” pattern. So, we create another state for that…

This is the rabbit hole I fell down. I am pretty sure it could be made to work, but it was complicated, and I wasted way to much time (see “sunk cost fallacy” for why that might happen) trying to figure out how to make it work, including how to track the number of different ways each pattern was matched.

It was dumb.

In hour three, I lost the train of thought, and wrote the following simple code to test my understanding of the problem and how it behaved on the simple test data.

def count(t):
    cnt = 0
    if t == '':
        return 1
    for p in patterns:
        if t.startswith(p):
            cnt += count(t[len(p):])
    return cnt

It burns through the simple test data in about 20ms. Of course I tried it on the real data and…

Well, it runs for a long time. In fact, it’s pretty much exponential in the length of the towels, and the large number of patterns doesn’t help either.

But suddenly I heard harps, and angels, and light shown down on me from above, and the seraphim all proclaimed how stupid I was. Ten seconds and a two line change later, I had the answer.

#!/usr/bin/env python

# okay, we can't leverage the re library this time..

data = open("input.txt").read()

patterns, towels = data.split("\n\n")

patterns = patterns.split(", ")

towels = towels.rstrip().split("\n")

from functools import cache

@cache
def count(t):
    cnt = 0
    for p in patterns:
        if t == '':
            return 1
        if t.startswith(p):
            cnt += count(t[len(p):])
    return cnt

total = 0
for t in towels:
    cnt = count(t)
    print(cnt, t)
    total += cnt

print(total)

I think if I had half the knowledge I’ve accumulated over the years, I would have solved this immediately. But instead I solved it 2h46m in, netting me a ranking of just 6847. An opportunity squandered.

Had I stepped back and actually looked at the simplicity of the problem, and remembered the use of caching/memoization (which I considered earlier, but without clarity of thought) I would have seen it for the simple problem it was.

Four decades of programming in, and I’m still learning. And re-learning. And un-learning.

Happy holidays all.