A friend of mine was working on a programming exercise, and it turns it out was based on a chunk of math which I thought I should have seen before, but either have not seen or have forgotten. It’s basically that the products of all primes less than some number n is less than or equal to en and in the limit converges to precisely en. First of all, I wrote a chunk of code to test it out, at least for primes less than a million. Here’s the code I wrote (I swiped my rather bizarre looking prime sieve code from a previous experiment with different sieving algorithms):
[sourcecode lang=”python”]
from random import randint
from math import sqrt, ceil, floor, log
import time
import sys
from math import *
def sieveOfErat(end):
if end < 2: return []
#The array doesn’t need to include even numbers
lng = ((end/2)-1+end%2)
# Create array and assume all numbers in array are prime
sieve = [True]*(lng+1)
# In the following code, you’re going to see some funky
# bit shifting and stuff, this is just transforming i and j
# so that they represent the proper elements in the array
# Only go up to square root of the end
for i in range(int(sqrt(end)) >> 1):
# Skip numbers that aren’t marked as prime
if not sieve[i]: continue
# Unmark all multiples of i, starting at i**2
for j in range( (i*(i + 3) << 1) + 3, lng, (i << 1) + 3):
sieve[j] = False
# Don’t forget 2!
primes = [2]
# Gather all the primes into a list, leaving out the composite numbers
primes.extend([(i << 1) + 3 for i in range(lng) if sieve[i]])
return primes
sum = 0.
for p in sieveOfErat(1000000):
sum += log(p)
print p, sum/p
[/sourcecode]
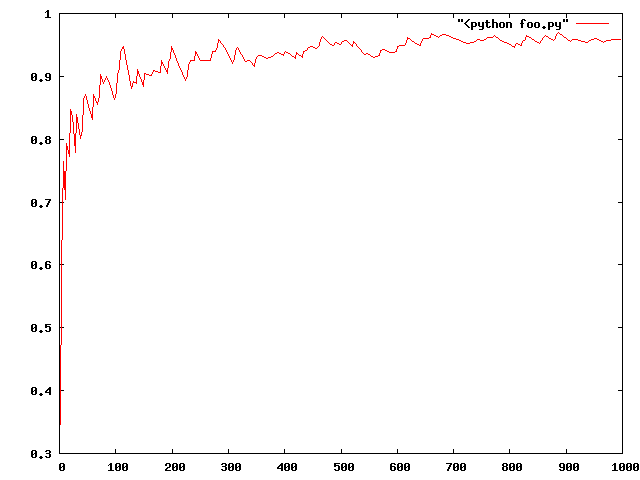
Most of the code is just the sieve. In the end, instead of taking a very large product, we instead take the logarithm of both sides. This means that the sum of the logs should be nearly equal to n. The program prints out the value of the prime, and how sum compares to the value of p. Here’s a quick graph of the results:
Note, it’s not monotonically increasing, but it does appear to be converging. You can run this for higher and higher values and it does appear to be converging to 1.
This seems like a rather remarkable thing to me. The relationship between e and primes seems (to me) completely unobvious, I wouldn’t have any idea how to go about proving such a thing. A quick search on Wikipedia reveals this page on the primorial function but similarly gives little insight. Recalling Stirling’s approximation for ordinary factorials suggests that these large products are related to exponentials (Stirling’s approximation not only has a factor of e in it, but also the square root of two times pi as well), but the idea that the product of primes would precisely mimic powers of e seems deeply mysterious…
Any math geniuses out there care to point me at a (hopefully simple) explanation of why this might be? Or is the explanation far from simple?
The limiting case when n is itself prime is a simple argument, given in Ruiz, S. M. “A Result on Prime Numbers.” Math. Gaz. 81, 269, 1997. I suspect that the extension of this limiting case to when n is not prime is trivial, but the proof of the inequality for all n may be a little different, possibly more difficult.
A sketch of the argument goes as follows. Suppose that n is the mth prime number p_n. The prime number theorem says that the size of p_m is asymptotically m*log(m). For large m, this is dominated by the m term, and so the product of the first m primes is m! (times a whole load of log terms, which turn out to be unimportant for large m). By Stirlings formula, m! ~ exp(m*log(m)), which (using the prime number theorem again) is asymptotically equal to exp(p_m). Thus the product of the first n primes is asymptotically equal to the exponential of the nth prime.
Another way of looking at it is that it’s equivalent to the claim that the Chebyshev function:
psi(x) = sum { log p | p prime, p^k 1 as x goes to infinity.
Again, this follows from the prime number theorem. Of course, it’s the prime number theorem itself which is nontrivial to prove.