Milhouse muses from the past…

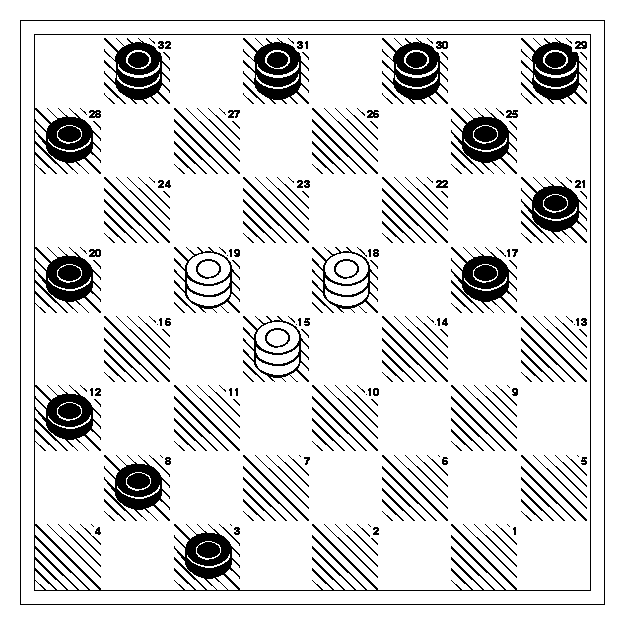
A couple of years ago, I mused about an “easy” checkers problem which my checkers program Milhouse found to be pretty difficult. Here’s the position again, with White to move and win:

An easy hard problem, or a hard easy problem?

(I didn’t mention the source of the puzzle before, I got it out of one of Rob Pike’s books, not sure which one. It’s puzzle 104 in my collection, but listed as Rob Pike Puzzle #8). As I mentioned before, it takes a fairly deep search to find the solution (28 plies). I had mentioned before that using the MTD(f) algorithm proposed by Plaat would find the solution very quickly, but that my implementation of alpha beta struggled significantly. I thought I’d try this position again to see what headway has been made in two years. Using the normal settings… here’s the output of iterative deepening….

      +1 : [-1038] 0.02s
         : 15-10
      +3 : [-1044] 0.02s
         : 18-14 30-26 14-10
... researching after failing low (-1070)
      +5 : [-1070] 0.02s
         : 15-10 32-27 19-23 28-32 23-19
      +7 : [-1086] 0.02s
         : 18-14 32-27 15-10 27-23 19x26 30x23 10-15
      +9 : [-1106] 0.04s
         : 18-14 30-26 15-10 32-27 19-15 25-30 14-9  28-32  9-14
     +11 : [-1118] 0.13s
         : 15-10 32-27 19-15 12-16 18-14  8-11 15x8   3x12 14-9 
         : 28-32  9-5 
     +13 : [-1133] 0.53s
         : 18-14 32-27 15-10 27-23 19x26 30x23 14-9  25-30  9-5 
         : 31-27 10-6  28-32  6-1 
     +15 : [-1143] 2.18s
         : 18-14 32-27 15-10 27-23 19x26 30x23 14-9  25-30  9-5 
         : 30-26 10-14 31-27 14-10 28-32 10-15
     +17 : [-1143] 8.53s
         : 18-14 32-27 15-10 27-23 19x26 30x23 14-9  25-30  9-5 
         : 30-26 10-14 28-32
... researching after failing low (-1168)
     +19 : [-1168] 46.67s
         : 15-10 32-27 18-14 28-32 14-9  31-26  9-5   8-11  5-9 
         : 17-22 19-24  3-7  10x3  27-23  9-5  20x27
     +21 : [-1176] 143.75s
         : 15-10 30-26 18-22 32-27 22x13  8-11 10-14 27-23 13-9 
         : 23x16  9-5  31-27  5-1

In other words, after two and a half minutes of searching, the computer still thinks white is screwed, with a score of -1176.

I wanted to go back and re-enable the MTD(f) algorithm in milhouse, but somehow through the 100 or so modifications that I’ve done since then, I’ve removed that code entirely. But I thought that I might make some small modifications to the program that would significantly enhance its ability to solve this puzzle. Milhouse normally uses a windowed search to find the best move using iterative deepening. It searches at increasing levels. Each time, it sets alpha and beta (the search window) to be centered around the current value with a search window witdth of about one quarter of a man. If the search returns inside that window, we know its precise value. If it returns less, we “fail low”, and if we really wanted to know what the value was, we’d have to re-search to find it by using different bounds (I normally use -INF to the new failed bound). Similarly, if it fails high, we might need to research.

But in our case, we don’t really care if we fail low. We know if we do that no winning solution can be found at that depth. There is no reason to try to find the exact value, we may as well just deepen the search and try again. So, I made some minor modifications to the iterative deepening procedure. I basically set the alpha cutoff to a high value (say 1000), and if we fail low, then we just continue without researching at the next depth. This is very similar to what mtd(f) does, except that it uses null-width searches. Here’s the trace:

... researching after failing low (-1038)
... researching after failing low (-935)
... researching after failing low (-926)
... researching after failing low (-818)
... researching after failing low (-722)
... researching after failing low (-715)
... researching after failing low (-616)
... researching after failing low (-602)
... researching after failing low (0)
... researching after failing low (0)
... researching after failing low (0)
... researching after failing low (0)
... researching after failing low (0)
... researching after failing low (222)
     +29 : [9973] 1.76s
         : 19-24 20x27 18-22 17x26 15-10  8-11 10-6   3-7   6-9 
         : 12-16  9-6  16-19  6-2  19-24  2-6  11-16  6-9  16-19 
         : 9-13 19-23 13-9   7-10  9-13 10-15 13-17 15-18 17-22
final score = 9973
1.757 seconds elapsed.

In other words, in less than two seconds, it finds the winning line. Very cool.