I had a project in mind for the Gameduino, part of which requires the display of a world map. But the Gameduino has a relatively limited amount of memory, and the “background” graphics is character mapped: instead of providing complete flexibility to plot individual points, the Gameduino memory is organized as a 64×64 array of 8 bit memory, each specifying a single 8×8 character. Thus, to make a “map”, we need to generate a character set and then build the resulting image out of those characters.

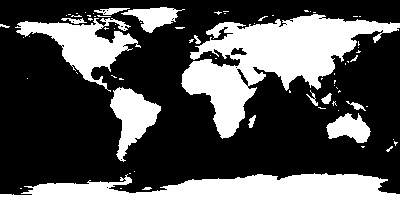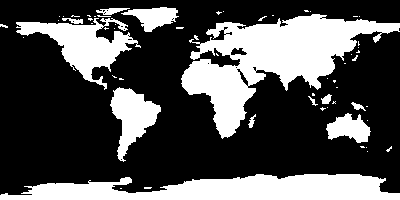
I began with a 400×200 map that I shrunk down from the image I got from this page and converted to a simple black and white image. I then tried to see how many unique 8×8 tiles there were: in this case, 342 unique tiles were needed to reproduce the image exactly.

But I don’t need to reproduce the image exactly, I just want as close an image as I can find, encoded with as few characters as I can find. I suspect that if I wanted to think about this hard, I could figure out a way to use some fairly strong bit of math to find a good solution. The problem would seem to be a binary vector quantization problem: each tile can be viewed as a 64 element binary vector. The problem is to find a set of 64 bit code words that approximate the distribution of codewords from the image tiles.

But of course I am lazy. When confronted with problems like this, I like to use techniques like simulated annealing to solve them. In fact, I coded up a pretty straightforward hill climbing algorithm. It simply takes a subset of (say) 128 tiles, and sees how closely it can approximate the image using those tiles. In each iteration, it swaps one of the tiles out for a different one, and keeps the new mapping if it lowers the number of error bits. A proper simulated annealing schedule would probably help, but even as slow and inefficient a scheme as it is, it still does a good job.

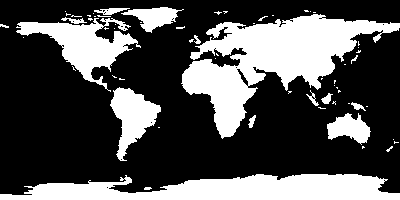
Here’s an animated gif that flips between the target and the image that I discovered that can be encoded with 128 characters. That still leaves 128 characters to use for, well, alphabets and numbers and the like. Looks pretty good.

I might work a bit more on this, to see if I can get a small bit better, but it’s useable for now.

Addendum: I added a few things that made it a bit better. The previous best map had about 650 bits different. I implemented a simple annealing schedule in my optimizer, and allowed it to use tiles which were not already in the existing pool by simply modifying tiles with single bit changes. This resulted in an image which has only 460 bits different. It’s annoying that it created a new “island” off the east coast of South America, but it’s still pretty good.

Addendum²: Oops, the reason this worked out better is that it uses 192 characters instead of 128. I was playing with different settings as I made changes. 192 characters is the max I could use in this application. That leaves 64 codes, which nicely covers the ASCII codes from 32 (space) to 95 (underscore) and includes all the capital letters and numbers.