Well, it wasn’t so much a difficulty with the Hilbert transform as a difficulty with my understanding. But with the help of my good friend Tom, my understanding was soon put right, and I thought it might make an interesting (in other words, horribly boring to anyone but myself) post, and at the very least, it would be good for me to document this little bit of mathematical fun.
Warning: complex numbers ahead!
This came up as a subtask of my slow scan television decoder. I’ll probably have a more detailed posting regarding the underlying theory, but the basic idea is as follows. The “pure” (without noise) SSTV signal is a frequency modulated signal with constant amplitude. But what does that really mean? After all, the instantaneous value of the signal varies: it’s a sine wave after all. What’s useful is to think of the analytic signal. Instead of being a single value at each moment in time, we think of a signal as a complex number, with a real and imaginary part. Let’s say the real part is $latex a$, and the imaginary part is $latex b$. The analytic signal can be represented as the complex number $latex a+b\imath$. The amplitude of the signal is then the $latex \sqrt{a^2+b^2}$.
If doesn’t make any sense to you, don’t fret. It’s mostly because we do a horrible job of teaching complex numbers, and I haven’t really done any better. You might be thinking, “what does this have to do with actual signals? The signals that I have are described by a single value, which varies over time. Why are you hurting my brain with complex numbers?”
In an attempt to stimulate you to think about it more, I’ll respond with the Socratic method, and as “what does the amplitude of a signal mean if they are described by only a single value?” In particular, how can you tell if a signal is “constant amplitude”? What does that even mean?
Okay, I’ll drop that topic for another time. Let’s just imagine that you accept my definition of constant amplitude, and we want to construct a complex signal from the real valued signal we receive from the radio. Let’s just pretend that the input signal gets copied into the real portion of the complex signal. In other words, the put values become the values for $latex a$ in our $latex a+b\imath$ above. For the purposes of our discussion, let’s say that the signal is some sine wave, $latex sin(t)$, where $latex t$ is a time variable (we could scale it to make it higher and lower frequency if we like). Let’s say the we’d like the amplitude of that signal is 1. Can we find values for $latex b$ that makes the amplitude $latex \sqrt{a^2+b^2} = 1$? If we square both sides, we see that $latex a^2 + b^2 = 1$, and since $latex a = sin(t)$, we see that $latex b^2 = 1-sin^2(t)$. If you remember any of your high school trig, you might remember that make $latex b = cos(t)$ ($latex sin^2(t) + cos^2(t) = 1$).
What this means is that for any given sine wave at a given frequency, we can get the complex version of the signal by copying a cosine signal of the same frequency into the imaginary part. If you think of cosine as just a phase with a 90 degree phase shift, you’ll see that if we had a magic filter that could make a 90 degree phase shift, you could easily construct the complex signal from the real signal.
But what if our signal isn’t made up of sine waves? Well, you can decompose the signal into the sum of a bunch of different sines (and cosines) of varying amplitude (proof left for the motivated reader). Applying the magic 90 degree phase shifter to all the sines, and then adding them back up, we’ll get the imaginary part of the signal we need.
None of this has anything to do with the problem really, it’s just background. It’s remarkably hard to explain this stuff to anyone who doesn’t understand it already, and I fear I’ve not done anything good. Oh well, onto my problem.
The way that you can implement the 90 degree phase shifter is by using some magic called the Hilbert transform, which can be implemented as an FIR filter. I wanted to create a black box that I feed values of my real signal in, and get (after some delay) the complex signal out. The code isn’t all that hard really, I’ll go ahead and put it here:
[sourcecode lang=”C”]
#include <stdio.h>
#include <stdlib.h>
#include <complex.h>
#include <math.h>
#define NZEROS (50)
static float xv[NZEROS+1];
static float yv[NZEROS+1];
static float xcoeffs[NZEROS+1] ;
double
window(int n, int N)
{
double a0 = 0.355768 ;
double a1 = 0.487396 ;
double a2 = 0.144232 ;
double a3 = 0.012604 ;
return a0 – a1 * cos(2.0 * M_PI * n / (N – 1))
+ a2 * cos(4.0 * M_PI * n / (N – 1))
– a3 * cos(6.0 * M_PI * n / (N – 1)) ;
}
void
oddhilb (float *hilb, int n)
{
float f;
int i, j, k, m;
m = j = k = (n – 1) >> 1;
for (i = 1; i <= m; i += 2) {
f = 2.0 / (i * M_PI) ;
hilb[j++] = 0.0;
hilb[j++] = f;
hilb[k–] = 0.0;
hilb[k–] = -f;
}
/* and now… window it…
*/
FILE *fp = fopen("unwindowed.dat", "w") ;
for (i=0; i<=n; i++)
fprintf(fp, "%lf\n", hilb[i]) ;
fclose(fp) ;
for (i=0; i<=n; i++) {
hilb[i] *= window(i, n+1) ;
}
fp = fopen("windowed.dat", "w") ;
for (i=0; i<=n; i++)
fprintf(fp, "%lf\n", hilb[i]) ;
fclose(fp) ;
}
complex
filterit(float val)
{
float sum;
int i;
for (i = 0; i < NZEROS; i++) {
xv[i] = xv[i+1];
yv[i] = yv[i+1];
}
xv[NZEROS] = val ;
for (i = 0, sum = 0.; i <= NZEROS; i++)
sum += (xcoeffs[i] * xv[i]);
yv[NZEROS] = sum ;
return xv[NZEROS/2] + I * yv[NZEROS] ;
}
main(int argc, char *argv[])
{
float f ;
complex c ;
int i ;
double t = 0. ;
oddhilb(xcoeffs, NZEROS+1) ;
for (i=0; i<4000; i++) {
f = sin(t) ;
t += 0.5 ;
c = filterit(f) ;
printf("%lf %lf\n", creal(c), cimag(c)) ;
// printf("%lf\n", cabs(c)) ;
}
}
[/sourcecode]
The program implements the Hilbert transform as an FIR filter. At each step, we compute a new value $latex f$ for our input signal. We then pass it to our filter stage, which returns our complex valued signal. If we then plot the real and imaginary parts of our signal, we should get a circle. And, in fact we do, now:
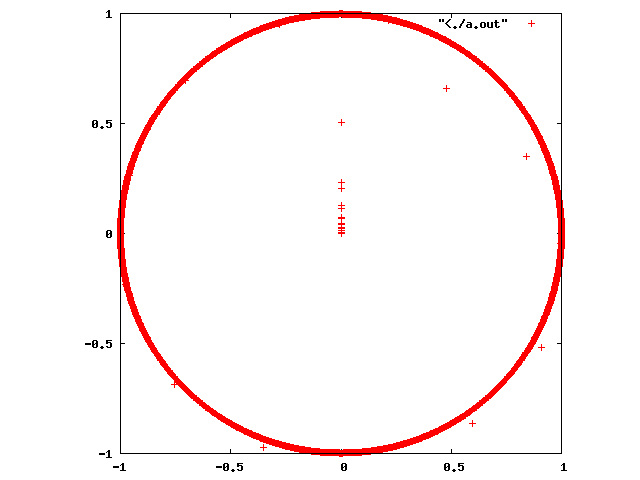
But when I started, I didn’t. The radius of the circle varied over quite a bit (maybe 10% or so). The reason was I forgot to apply the windowing function to the Hilbert transform filter coefficients. Plotting the two sets of coefficients, we see that the filtered versions fall to zero faster away from the middle.
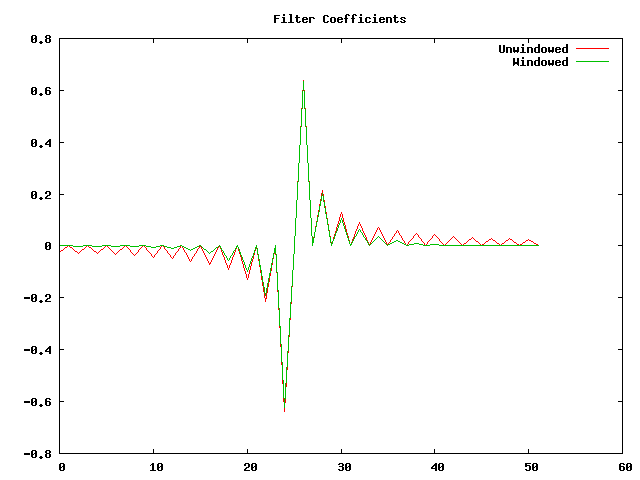
We can use the FFT on these coefficients to see what the frequency response is.
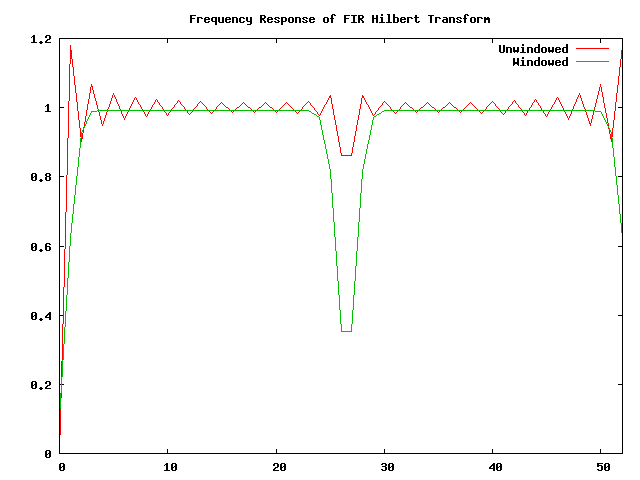
You can see that the unwindowed filter has very uneven response over the range of frequencies, while the windowed signal is nice and flat over all but the region very near zero and the Nyquist frequency. This means that when we feed it nice sine waves, we’ll get a nice analytic signal with very constant amplitude.
Addendum(s): There is a small “off by one” error that adds an extra zero coefficient to the filters above. I’ll tidy it up a bit more when I get a chance. As Tom pointed out, for use in my SSTV decoder, it’s almost certain that just 11 coefficients would work just fine (and be faster). We could also optimize out the multiply by zeros in the convolution.