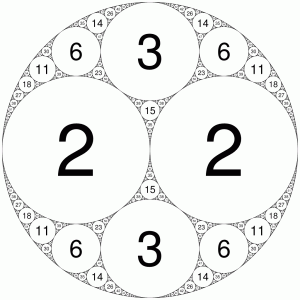
It took me an embarrassingly long time to write a program to generate this fractal known as the Apollonian Gasket:
More information here:
Apollonian gasket – Wikipedia, the free encyclopedia
Each circle is labelled with its curvature (which is simple the reciprocal of the radius). In this particular instance, all the curvatures turn out to be integers. Not really sure why I think this is interesting, but there you are.
Very cool, I was inspired to try doing this (and other shapes) myself by Vihart’s YouTube video:
http://www.youtube.com/watch?v=DK5Z709J2eo
But like so many things has been enqueued with low priority.
This provided at least 10 minutes of intellectual stimulation – I glanced at the picture and asked myself: “Why can’t you use this to trisect an angle?” A little sketching revealed the answer; you can’t draw it without trisecting angles.
It turns out to be the case that any Apollonian gasket with four mutually tangent circles of integer curvature has integer curvature for all its circles.
http://en.wikipedia.org/wiki/Apollonian_gasket
There was a Science News article some time ago about Apollonian circle packings which I think came out shortly after this had been proved.
Pingback: Gasketch v1 released! | Joey.Cloud