My previous entry talked about the problems that I’ve been having with the Anet A8. I haven’t had the time to actually do some rework of the connector (I should get to that later today) but while I was commuting I thought about it a bit, and was trying to answer the following questions.

• How much resistance would this bad connection need to add to affect the bed heating?
• How much power was being dissipated by the PCB and at the location of the bad joint?
• Was there a significant danger of a serious meltdown?

The way I approached this was to first get some data about the heated bed. Nominally, the bed is rated for 12V at 1.2 ohms resistance. Using Ohm’s law, we know that the current is voltage divided by resistance, so the total current draw should be 10 amps, and the power is current times voltage, so the power should be 120 watts.

If you look at the bed, you’ll see it consists entirely of a very long, thin, wide PCB track which winds around the 220x220mm surface. It dissipates the power as heat, and since the resistance of the track is (very nearly) uniform, you would expect the total power to be dissipated across the entire length of the track, providing relatively uniform and modest heating.

We can model this system as a simple voltage source as 12v DC, with a series load resistance of 1.2 ohms.

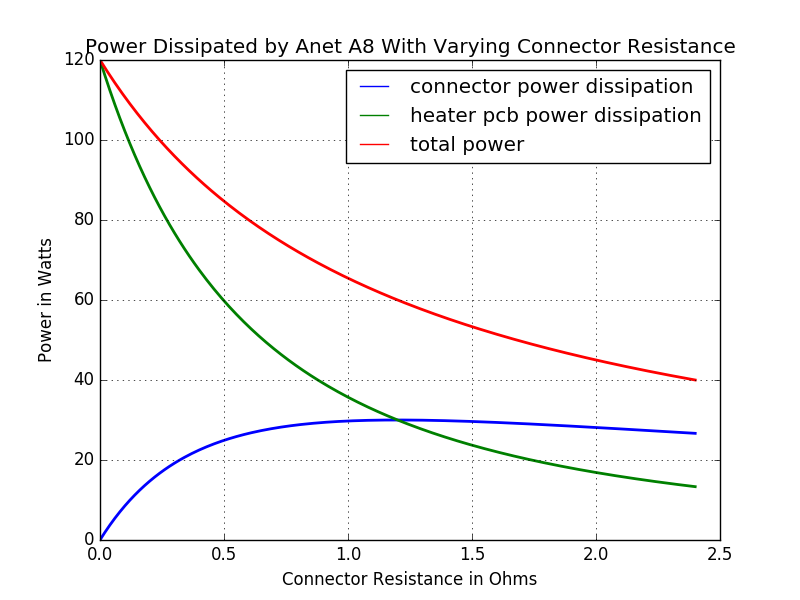
If we have a bad resistive connection to the heated bed, we have some additional resistance in series with our load resistance. The total current through the bed drops because the resistance is now the sum of the connector and load resistance, which means that the total power drops. (We will imagine that the supply will continue to provide 12v regulated for this experiment.) The total power is divided between the power dissipated by the bad connector and the heated bed. A little work with Ohm’s law and voltage dividers, and you can figure out how that power splits depending on the connector resistance. I could go through the math, but it’s basic intro DC stuff. I wrote a little scrap of Python and made a graph as I varied the connector resistance
through some low values.

You can see that at even pretty small resistances, the power to the heated bed starts to drop significantly. More than that though, the power dissipated by the connector grows pretty quickly. It actually reaches its peak when its resistance matches that of the bed, where the green and blue lines cross, indicating that the power dissipated by the bed and pcb are equal, and dissipate 30 watts each.

But from a practical standpoint it is important to remember that while the 30w of the bed is spread along its entire (and substantial length) the 30w dissipated by the connector is quite small, and thus there is likely to be significant (or even catastrophic) heating at the connector. It is also important to note that as the connector resistance grows beyond this point, the power curve drops slowly, so it might continue to heat significantly over a much larger range of resistance values.

So, my math indicates that I should really be concerned about connector resistance. I think this means that I am going to avoid using a connector entirely, and solder 12 AWG wire directly to the power terminals, and carefully measure the total resistance before and after. I will also provide some additional strain relief so that as the wire flexes, it doesn’t work the joint loose.

That’s the theory. Stay tuned for the rework.