brainwagon

Last year, I bodged together a motion detecting camera to photograph hummingbirds at my hummingbird feeder. But it was always a temporary hack. We had some difficulty with the ants that discovered the feeder, and we discontinued the experiment.

I had a post that I could hang some feeders from, and decided to fill a planter with cement and embed the post so I could move it around and hose it down easily. It’s working pretty well: last weekend we finished it, and have already had to refill the feeder. I think I’ve identified at least three to four hummingbirds who are feeding there, although they seem quite territorial, and one of the larger ones often scares off the smaller ones.

But he doesn’t seem to bother this guy:

I’m not much of a bird watcher, but a little googling suggests to me that he’s a Hooded Oriole. They seem to like the sugar water from hummingbird feeders, and slurp up a fair amount of this stuff when they land. I’ve seen a female of the species as well, who is a bit paler and lacks the black markings surrounding the eye.

I’ll try to get the motion detecting camera up sometime in the next few weeks.

Long time readers of this blog might remember that I received a Gameduino board designed by James Bowman. I used it to construct ANGST, an Arduino and Gameduino satellite tracking project. James did all the heavy lifting: the Gameduino uses a Xilinx FPGA to implement an Arduino shield that can generate graphics and sounds. To do so, it actually implements a “soft processor”, a very simple CPU core designed to execute the Forth Programming Language. I enjoyed goofing around with it, but it’s been sitting in a box for quite a while.

A couple months ago, I remember hearing about an interesting project called Project IceStorm. One of the things that has kept me from tinkering with FPGAs is that the development environments are proprietary and big. Really big. Wrapping my head around them just didn’t seem like fun. But Project Icestorm tries to apply open source methodology to FPGA programming. They reverse engineered the bitstream used by a simple family of FPGAs made by Lattice Semiconductor. The result is a complete set of tools to code logic designs in Verilog, compile, place, route and download them to a Lattice FPGA board. What’s doubly cool is that James took the core of his J1a processor and adapted it for a very cheap Lattice IceStick development board. Compared to some other FPGA boards, the Lattice ICE40 chips are pretty limited, but the J1a is a pretty good fit, and now with Project IceStorm, you can compile and download directly to the board, and have a small Forth base system running without any extra hardware.

I went ahead an ordered one of the boards, and following the instructions on James’ website, I went ahead and built the code and successfully installed in on my $21 ICESTICK. Initially, I had some trouble running the LED blink test: three of the leds worked fine, but two wouldn’t seem to light. Eventually, I tried updating the “yosys” software and recompiling it, and after that, it worked as expected. I’ve never done any Verilog programming before, but having this setup seems to make it seem more tractable than it has before. I’m dusting off the largely unused Verilog books I have on my shelf, and am thinking of trying something simple like a digital clock as my first try. I suspect I’ll outgrow the ICESTICK pretty quickly, but until I do, I bet I am going to learn a lot.

James does a better job describing his system than I could, so here’s a link to his video and his page describing the system. Thanks to Ken Boak for also drawing my attention to this project.

James’ page on J1a SwapForth

Joel Grus blogged about a job interview where he was asked about the ridiculous Fizz Buzz question that apparently some companies use to weed out complete frauds from their job interview process. The task is to create a program which prints the numbers from 1 to 100, but where all numbers which are a multiple of three are replaced with “fizz”, all numbers which are multiples of five are replaced with “buzz” and all numbers which are multiples of both three and five are replaced by “fizzbuzz”.

Joel somewhat comically decided to use the TensorFlow framework and solve it with machine learning. Go read his post, it’s pretty comical. Well, if you are a programming geek, it will seem comical.

For the non programmers in my audience (are there some?) this is a trivial program to write. If a programmer can’t bust out a solution to this in a minute or two, they likely have no business calling themselves a programmer. Here’s my 30 second solution (I type moderately slow):

[sourcecode lang=”cpp”]
#include <stdio.h>

int
main()
{
int i ;
for (i=1; i<=100; i++) {
if (i % 15 == 0) {
printf("fizzbuzz\n") ;
} else if (i % 3 == 0) {
printf("fizz\n") ;
} else if (i % 5 == 0) {
printf("buzz\n") ;
} else {
printf("%d\n", i) ;
}
}
return 0 ;
}
[/sourcecode]

No doubt there are some practitioners in the audience who think that this inefficient, because I compute multiple modulo operations per loop iteration. I’d probably argue that this is short and clear, and until profiling revealed it to be a performance problem, I wouldn’t change it. If people insisted that I do a single modulo per loop iteration, I’d probably replace it with something like:

[sourcecode lang=”cpp”]
#include <stdio.h>

int
main()
{
int i ;
for (i=1; i<=100; i++) {
switch (i % 15) {
case 3:
case 6:
case 9:
case 12:
printf("fizz\n") ;
break ;
case 5:
case 10:
printf("buzz\n") ;
break ;
case 0:
printf("fizzbuzz\n") ;
break ;
default:
printf("%d\n", i) ;
break ;
}
}
return 0 ;
}
[/sourcecode]

I’d submit that it is much less clear, but not too bad. I’d probably add a comment to explain the higher level idea.

If we are allowed two modulo calls per iteration, could do it this way:

[sourcecode lang=”cpp”]
int
main()
{
int i ;
for (i=1; i<=100; i++) {

bool mul3 = (i % 3 == 0) ;
bool mul5 = (i % 5 == 0) ;

if (mul3 && mul5) {
printf("fizzbuzz\n") ;
} else if (mul3) {
printf("fizz\n") ;
} else if (mul5) {
printf("buzz\n") ;
} else {
printf("%d\n", i) ;
}
}
return 0 ;
}
[/sourcecode]

I used boolean variables, which I think reads a little better, but you could obviously use integers.

What if you don’t want to any modulus calls? Well, you could use a state machine…

[sourcecode lang=”cpp”]
#include <stdio.h>

int
main()
{
int i = 1 ;
int state = 1 ;

while (i <= 100) {
switch (state) {
case 3:
case 6:
case 9:
case 12:
printf("fizz\n") ;
break ;
case 5:
case 10:
printf("buzz\n") ;
break ;
case 15:
printf("fizzbuzz\n") ;
state = 0 ;
break ;
default:
printf("%d\n", i) ;
}
state ++ ;
i++ ;
}
return 0 ;
}
[/sourcecode]

I hope I never have an interview where this is the kind of question I get asked.

I just recently found out about the /r/showerthoughts subreddit, where people vote on pithy sayings. I thought this might be a fun thing to have to replace the aging and relatively static “fortune” file that I use. I used the Python “PRAW” library to fetch the top entry for the day, and then optionally pass it to the terrific “cowsay” program for formatting.

Here’s the tiny, nearly trivial code, whose code includes an example of the output of “./shower –cow”

[sourcecode lang=”python”]
#!/usr/bin/env python
# -*- coding: utf-8 -*-

# a program for fetching texts from Reddit’s /r/showerthoughts reddit.
# _________________________________________
# / The guy who said “Look! Up in the sky! \
# | It’s a bird!” in the Superman intro was |
# \ strangely excited to see a bird… /
# —————————————–
# \ ^__^
# \ (oo)\_______
# (__)\ )\/\
# ||—-w |
# || ||

# Written by Mark VandeWettering, no rights reserved.

import sys
import subprocess
import argparse
import textwrap
import praw

parser = argparse.ArgumentParser(description = ‘Fetch shower thoughts from reddit.’)
parser.add_argument(‘–cow’, action=’store_true’,
help=’pipe output through cowsay’)
parser.add_argument(‘–cowstyle’, dest=’cowstyle’, nargs=1, default=[‘default’],
help=’style passed to cowsay’)
args = parser.parse_args()

r = praw.Reddit(‘shower’)
s = r.get_subreddit(‘showerthoughts’)

submissions = s.get_top_from_day(limit = 1)

for submission in submissions:
if args.cow:
ps = subprocess.Popen([‘cowsay’, ‘-f’, args.cowstyle[0]], shell=False, stdin=subprocess.PIPE)
ps.stdin.write(submission.title.encode(‘utf-8’))
ps.stdin.close()
ps.wait()
else:
for l in textwrap.wrap(submission.title, 60):
print ("\t%s" % l).encode(‘utf-8’)
[/sourcecode]

The other day I mentioned that generating random Latin squares was a bit more complicated than I thought, and that an algorithm by Jacobson and Matthews was the way that people typically did it. I worked up this implementation based on a couple of different descriptions of the algorithm (the original paper was behind a paywall). The code below simply generates a random DIMxDIM Latin square using their algorithm. I haven’t done extensive testing, but it appears to mostly work. I did run a test where I generated one million 4×4 matrices, and found that it generated all 576 different matrices in approximately the same propertion, so it appears to at least be roughly operational. I’ll eventually merge the code with my nascent KenKen generator.

[sourcecode lang=”cpp”]
#include <stdio.h>
#include <stdlib.h>
#include <unistd.h>

/*
* rls.c
*
* A straightforward implementation of the algorithm by Jacobson and
* Matthews, _Generating uniformly distributed random Latin square_,
* Journal of Combinatorial Design, 1996.
*
* I actually couldn’t find the original paper, so this is an implementation
* based upon other descriptions of the algorithm.
*
* Written by Mark VandeWettering.
*
*/

#define DIM (6)

typedef struct t_incidence_cube {
int s[DIM][DIM][DIM] ;
} IncidenceCube ;

void
InitIncidenceCube(IncidenceCube *c)
{
int i, j, k ;

/* First, zero the cube */
for (i=0; i<DIM; i++)
for (j=0; j<DIM; j++)
for (k=0; k<DIM; k++)
c->s[i][j][k] = 0 ;

/* And then dump ones in the right place… */
for (i=0; i<DIM; i++)
for (j=0; j<DIM; j++)
c->s[i][j][(i+j)%DIM] = 1 ;
}

void
PrintIncidenceCube(IncidenceCube *c)
{
int i, j, k ;

for (i=0; i<DIM; i++) {
for (j=0; j<DIM; j++) {
for (k=0; k<DIM; k++) {
if (c->s[i][j][k]) {
printf("%2d ", k+1) ;
break ;
}
}
}
printf("\n") ;
}
printf("\n") ;
}

void
CompactPrintIncidenceCube(IncidenceCube *c)
{
int i, j, k ;

for (i=0; i<DIM; i++) {
for (j=0; j<DIM; j++) {
for (k=0; k<DIM; k++) {
if (c->s[i][j][k]) {
printf("%01d", k+1) ;
break ;
}
}
}
}
printf("\n") ;
}

void
ShuffleIncidenceCube(IncidenceCube *c)
{
int i, j ;

for (i=0; i<DIM*DIM*DIM; i++) {

// Assume we have a "proper" matrix…

// Pick a random zero from the incidence cube…
int rx, ry, rz ;
do {
rx = lrand48() % DIM ;
ry = lrand48() % DIM ;
rz = lrand48() % DIM ;
} while (c->s[rx][ry][rz]) ;

int ox, oy, oz ;

for (j=0; j<DIM; j++) {
if (c->s[j][ry][rz] == 1)
ox = j ;
if (c->s[rx][j][rz] == 1)
oy = j ;
if (c->s[rx][ry][j] == 1)
oz = j ;
}

// do the +/- 1 move…
// These are all square with zeros in them…
c->s[rx][ry][rz] ++ ;
c->s[rx][oy][oz] ++ ;
c->s[ox][ry][oz] ++ ;
c->s[ox][oy][rz] ++ ;

// These all have ones, except for maybe the last one…
c->s[rx][ry][oz] — ;
c->s[rx][oy][rz] — ;
c->s[ox][ry][rz] — ;
c->s[ox][oy][oz] — ;

while (c->s[ox][oy][oz] < 0) {

rx = ox ;
ry = oy ;
rz = oz ;

// Pick one of the two 1’s that are in conflict
if (drand48() < 0.5) {
for (j=0; j<DIM; j++) {
if (c->s[j][ry][rz] == 1) {
ox = j ;
}
}
} else {
for (j=DIM-1; j>=0; j–) {
if (c->s[j][ry][rz] == 1) {
ox = j ;
}
}
}

if (drand48() < 0.5) {
for (j=0; j<DIM; j++) {
if (c->s[rx][j][rz] == 1) {
oy = j ;
}
}
} else {
for (j=DIM-1; j>=0; j–) {
if (c->s[rx][j][rz] == 1) {
oy = j ;
}
}
}

if (drand48() < 0.5) {
for (j=0; j<DIM; j++) {
if (c->s[rx][ry][j] == 1) {
oz = j ;
}
}
} else {
for (j=DIM-1; j>=0; j–) {
if (c->s[rx][ry][j] == 1) {
oz = j ;
}
}
}

// do the +/- 1 move…
// These are all square with zeros in them…
c->s[rx][ry][rz] ++ ;
c->s[rx][oy][oz] ++ ;
c->s[ox][ry][oz] ++ ;
c->s[ox][oy][rz] ++ ;

// These all have ones, except for maybe the last one…
c->s[rx][ry][oz] — ;
c->s[rx][oy][rz] — ;
c->s[ox][ry][rz] — ;
c->s[ox][oy][oz] — ;
}

}
}

int
main()
{
IncidenceCube c ;
int i ;

srand48(getpid()) ;
InitIncidenceCube(&c) ;
ShuffleIncidenceCube(&c) ;
PrintIncidenceCube(&c) ;
return 1 ;
}
[/sourcecode]

My last post dealt with a solver for KenKen puzzles. Once you have one of those, then the obvious thing to work on next (in your copious spare time) is a generator for KenKen puzzles. It didn’t seem too hard. You’d begin by generating a random Latin square, then divide it up into “cages”, assign an operator to them, and then see if that has a unique solution. If it doesn’t, well, try again.

But it turns out that each of these steps hides inner difficulties, as well as a certain amount of mathematical beauty. Tom and I were discussing the first bit (generating random Latin square) over lunch, and I thought I’d summarize some of our discussion.

First of all, consider the following “canonical” Latin square of order 4:

1 2 3 4
4 1 2 3
3 4 1 2 
2 3 4 1

It’s pretty easy to generate this Latin square, and it’s pretty easy to generate other Latin squares by swapping either rows or columns. But the question is, can I generate all other Latin squares from this one by doing row and column swap operations?

Tom assured me that the answer was no, which wasn’t at all apparent to me until he presented an interesting example, so I thought I would summarize some of the ideas here. My presentation will take a slightly different path than our discussion, but it ends in the same place.

Let’s consider each square to have a canonical form, where the first row and first column are in sorted order. It should be relatively obvious that you can place any matrix into this form by a series of row and column operations. For example, the matrix above can be placed in canonical form by swapping the second and fourth row.

1 2 3 4
2 3 4 1
3 4 1 2
4 1 2 3 

But let’s consider a different matrix in canonical form formed by swapping 1 and 3 in rows 2 and 4.

1 2 3 4
2 1 4 3
3 4 1 2 
4 3 2 1 

We can’t convert this matrix into the previous one by only swapping rows and columns. Thus, if we try to generate a random Latin square by just beginning with a canonical one, there are possible Latin squares which can never be generated by just swapping row and column operations. Too bad, since this is really easy to implement.

Another easy thing to implement would be to just generate all possible Latin squares, store them in a table, and select one at random. That doesn’t seem too bad, until you consider that there are 812,851,200 possible Latin Squares to consider. Sure, disks are big, but that seems excessive.

It turns out that the algorithm that most people seem to use is the from 1996 by Jacobson and Matthews, which is hard to find online as a full paper. It uses a similar idea, but instead of swapping full rows and columns, it applies a different operator that mutates a given Latin square, and in the limit produces a distribution which is the same as the random distribution. It’s a little tricky to understand, but I am going to try to have an implementation in Python later tonight.

Here’s a report that provides some details and the skeleton of an implementation in Java.

Lately, my lunch hours have been spent working on the NYT Crossword with my lunch companion Tom. While I find that the Thursday crosswords are often beyond my ability to do in the allotted time, between the two of us, more often than not we manage to plow through them. Slowly over time, we’ve begun to solve them slightly quicker, so I’ve branched out to doing the KenKen puzzles.

For those of you who haven’t seen these before, you can learn about them on their official website here. The 4×4 ones are usually pretty easy, but the last couple days have done some 6×6 puzzles have been shockingly hard. So much so, that today I got to this state on today’s puzzle:

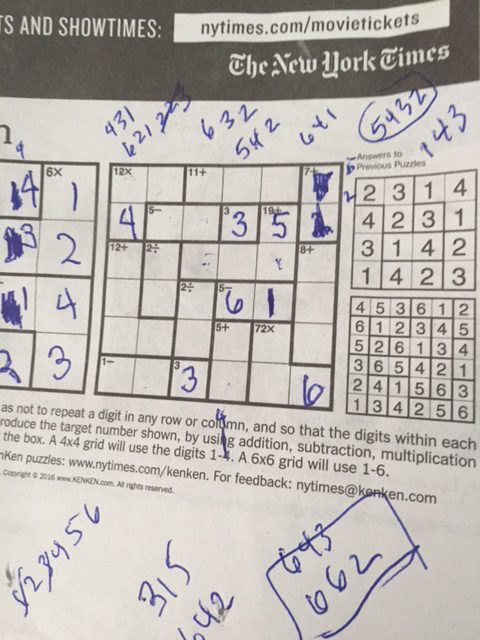
Yes, I was using pen. And I made a mistake, although I can’t see what I was thinking when I did. And because I made a mistake, I couldn’t spot it, and I was hung up. The “4” in first column was wrong. I knew it could not be a 6 or 1, or a 3, or a 4, but for some reason I thought that the final column couldn’t be 4 and 3, but..

Never mind, it doesn’t matter what the mistake was.

By the end up twenty minutes I was annoyed, knew I had made a mistake, but decided to give into the urge to write a program to solve it. How long could it take?

Well, the answer was about 27 minutes.

This program doesn’t have any interface or flexibility, everything is hard coded. Basically it uses backtracking and fills in each square in order from bottom left to top right, and as the top most, right most square of each outlined area is finished, it checks to make sure that the sums/differences/whatever for the filled in region sum to the right values. I didn’t know how I was going to encode those constraints, so I just ended up writing a function that computes the proper constraint. This is not really the right way to do it: it’s error prone and requires recompilation of the code to change the puzzle. But it does work fairly well, once you type the expressions in correctly.

Once I got those straightened out, it blats out the solution in less than 1 millisecond on my desktop.

+---+---+---+---+---+---+
| 6 | 1 | 5 | 2 | 4 | 3 |
+---+---+---+---+---+---+
| 2 | 6 | 1 | 3 | 5 | 4 |
+---+---+---+---+---+---+
| 1 | 4 | 6 | 5 | 3 | 2 |
+---+---+---+---+---+---+
| 3 | 2 | 4 | 6 | 1 | 5 |
+---+---+---+---+---+---+
| 5 | 3 | 2 | 4 | 6 | 1 |
+---+---+---+---+---+---+
| 4 | 5 | 3 | 1 | 2 | 6 |
+---+---+---+---+---+---+

1 solutions found

It points out that the 4 should have been a 2 (IDIOT!) and then it all works out.

The code is 178 lines long, but is not particularly pretty/short/adaptable. Some day, I’ll have to tidy it up and make a better version.

But in case people find this stuff interesting, here it is. Remember: 27 minutes to write.

[sourcecode lang=”cpp”]
include <stdio.h>
#include <stdlib.h>
#include <string.h>

/*
* kenken.c
*
* A program inspired by a particular tough 6×6 puzzle that appeared
* on Thursday, May 11, 2016, which Tom Duff and I could not appear to
* get the answer to during our lunch hour. I thought that it was possible
* that I could write a program to solve the puzzle in less than an hour.
*
* Hence, this code.
*
*/

int total = 0 ;

#define DIM (6)

typedef struct t_puzzle_state {
int sq[DIM][DIM] ;
int r[DIM] ; // bitflag for values left in rows…
int c[DIM] ; // bitflag for values available in columns
} PuzzleState ;

void
PrintPuzzleState(PuzzleState *p)
{
int i, j ;

printf("+") ;
for(j=0; j<DIM; j++)
printf("—+") ;
printf("\n") ;

for (i=0; i<DIM; i++) {
printf("|") ;
for (j=0; j<DIM; j++) {

if (p->sq[DIM-1-i][j])
printf(" %1d |", p->sq[DIM-1-i][j]) ;
else
printf(" |") ;
}
printf("\n+") ;
for(j=0; j<DIM; j++)
printf("—+") ;
printf("\n") ;
}
printf("\n") ;
}

void
InitializePuzzleState(PuzzleState *p)
{
int i, j ;

memset((void *) p, 0, sizeof(*p)) ;

for (i=0; i<DIM; i++) {
for (j=1; j<=DIM; j++) {
p->r[i] |= (1<<j) ;
p->c[i] |= (1<<j) ;
}
}
}

void
HardcodePuzzleState(PuzzleState *p, int r, int c, int val)
{
p->sq[r][c] = val ;
p->r[r] &= ~(1<<val) ;
p->c[c] &= ~(1<<val) ;
}

#define SQUARE(i, j) ((i)*DIM+(j))
#define ABS(x) ((x)<0?(-(x)):(x))

int
ConstraintSatisfied(PuzzleState *p, int i, int j)
{
switch (SQUARE(i,j)) {
case SQUARE(0,1):
return ABS(p->sq[0][0] – p->sq[0][1]) == 1 ;
case SQUARE(0,2):
return p->sq[0][2] == 3 ;
case SQUARE(1, 3):
return (p->sq[0][3]+p->sq[1][3]) == 5 ;
case SQUARE(1, 4):
return (p->sq[0][4] * p->sq[0][5] * p->sq[1][4]) == 72 ;
case SQUARE(2, 2):
if (p->sq[2][2] == 2 * p->sq[1][2])
return 1 ;
if (p->sq[1][2] == 2 * p->sq[2][2])
return 1 ;
return 0 ;
case SQUARE(2, 4):
return ABS(p->sq[2][4] – p->sq[2][3]) == 5 ;
case SQUARE(3, 1):
if (p->sq[3][1] == 2 * p->sq[2][1])
return 1 ;
if (p->sq[2][1] == 2 * p->sq[3][1])
return 1 ;
return 0 ;
case SQUARE(3, 5):
return (p->sq[3][5]+p->sq[2][5]+p->sq[1][5]) == 8 ;
case SQUARE(4, 2):
return ABS(p->sq[4][2] – p->sq[4][1]) == 5 ;
case SQUARE(4, 3):
return p->sq[4][3] == 3 ;
case SQUARE(4, 4):
return (p->sq[4][4]+p->sq[3][2]+p->sq[3][3]+p->sq[3][4]) == 19 ;
case SQUARE(5, 1):
return (p->sq[4][0]*p->sq[5][0]*p->sq[5][1]) == 12 ;
case SQUARE(5, 4):
return (p->sq[5][2]+p->sq[5][3]+p->sq[5][4]) == 11 ;
case SQUARE(5, 5):
return (p->sq[5][5]+p->sq[4][5]) == 7 ;
default:
return 1 ;
}

return 1 ;
}

void
SolvePuzzleState(PuzzleState *p, int i, int j)
{
int v ;

if (i >= DIM) {
PrintPuzzleState(p) ;
total ++ ;
return ;
}

int pval = p->r[i] & p->c[j] ;

for (v=1; v<=DIM; v++) {
if ((pval & (1<<v)) == 0)
continue ;
// Try to place v in sq[i][j] ;
p->sq[i][j] = v ;

if (ConstraintSatisfied(p, i, j)) {
p->r[i] &= ~(1<<v) ;
p->c[j] &= ~(1<<v) ;

int ni, nj ;
nj = j + 1 ;
if (nj < DIM) {
ni = i ;
} else {
ni = i + 1 ;
nj = 0 ;
}

SolvePuzzleState(p, ni, nj) ;

p->r[i] |= (1<<v) ;
p->c[j] |= (1<<v) ;
}
}
p->sq[i][j] = 0 ;
}

main()
{
PuzzleState p ;
InitializePuzzleState(&p) ;
// HardcodePuzzleState(&p, 0, 2, 3) ;
// HardcodePuzzleState(&p, 4, 3, 3) ;

SolvePuzzleState(&p, 0, 0) ;
fprintf(stderr, "%d solutions found\n", total) ;
}
[/sourcecode]

Just a pointer to a cool project which appeared on Hackaday: a solar powered FPV plane that can fly forever (or at least until the sun goes down). Pretty spiffy!

The comments show a link to this solar powered plane developed at ETH:

It was in the air for 81.5 hours, and had a continuous flight distance of 2316km. It’s a slow flyer: average speed is just under 18mph. At the end, you can see that the wind conditions had deteriorated seriously. Pretty nifty.

I’ve been meaning to write down this story for a while, because it represents a time when I was booed away from a microphone by a crowd of two thousand people, and I always think that stories like this are fun.

Back in 1996, I attended SIGGRAPH in New Orleans. I remember flying out early and arriving somewhere around 7:00AM and being unable to check into my hotel room, so I went down to the French Quarter and had beignets and coffee. It was a wonderful city for one of my favorite activities: eating. Pixar alumnus and foodie Steve Upstill had given out a list of restaurants in New Orleans for me to try, and I don’t think I had a bad meal the entire week. From gumbo to po’boy sandwiches, it was all amazing and delicious.

But back to the conference..

There was a panel that I attended called “Graphics PCs will Put Workstation Graphics in the Smithstonian”. The panelists were:

• Sam Uselton, from MRJ, Inc. served as organizer.
• Michael Cox, from S3
• Jay Tayborg, from Microsoft
• Michael Deering, from Sun Microsystems
• Kurt Akeley, from SGI

It was an interesting discussion, with the first two taking the the side of PCs, and the second two, standing up for the workstations. I had been working in scientific visualization at Princeton, and had then been at Pixar for about five years. My own opinions were that economies of scale would eventually destroy the workstation market. I had worked with high end SGI products, as well as workstations such as Stellar/Ardent/Stardent but had also been tracking the developments in the game world, and to me the writing on the wall was clear.

I remember approaching the microphone and asking a question like “Given what we’ve seen with Moore’s law and the increase in capabilities in microcomputers, and the increasing availability of operating systems like Linux and BSD-based systems,isn’t it reasonable to conclude that the same kind of thing will happen in the graphics market?”

I recall that Akeley and Deering tried to answer with something along the lines of “only workstations have the fast buses/high performance memory subsystems/careful and accurate rasterization that is necessary to do real graphics. I didn’t find that answer particularly helpful and tried to ask a followup and…

Was enthusiastically booed away from the microphone. It was really impressive, to have a couple of thousand people heckle you at once.

But in the end… I think that history points out that I was more or less correct. By no means did I contribute to this trend, but I did recognize it at the time, in a way that the majority of professionals at SIGGRAPH largely did not.

1995 was the apex for SGI, with a market cap of over 7 billion dollars. Ten years later, it was delisted from the NYSE because its stock price had fallen to below one dollar, with a market cap of just $120 million dollars. It was effectively bankrupt in 2006.

Sun would take a different path, riding the dot.com bubble up with its server hardware into the year 2000, and then riding it down to destruction. It never really became a big player in graphics.

Meanwhile, nVidia was formed in 1993 by Huang, Malachowsky and Priem (from AMD, Sun Micro and Sun Micro, respectively). In 1999 they released their Geforce board, which brought hardware with a full transform and light pipeline to the consumer market. They would absorb many other players, and became the destination for a lot of talent who had previously been at SGI. It currently has a market cap of about $18.6 billion dollars.

Mind you, nVidia didn’t pursue a strategy driven entirely by consumer products, and Sun and SGI failed not just because of their graphics strategy. But I do think that I what I said was mostly right, and it didn’t take forever for my prediction to come true.

Another press account of the session.

The summary page from the 1996 SIGGRAPH proceedings

Backtracking is a better technique, obviously. The version from earlier today was actually not very clever, and took half an hour to find the 73,712 solutions to the 13×13 checkerboard. This version is less code (just 91 lines, compared to 107 for yesterdays) and finds all the 13×13 solutions in just 2.5 seconds (a speed up of around 720x).

[sourcecode lang=”cpp”]
#include <stdio.h>
#include <stdlib.h>

#define MAX_N (15)

int board[MAX_N] ;
int total = 0 ;

void
print(int board[MAX_N], int n)
{
int i, j ;

printf("+") ;
for (i=0; i<n; i++) {
printf("-") ;
if (i < n-1)
printf("+") ;
}
printf("+\n") ;

for (i=0; i<n; i++) {
printf("|") ;
for (j=0; j<n; j++) {
if (j == board[i])
printf("O") ;
else
printf(" ") ;
if (j < n-1)
printf("|") ;
}
printf("?\n") ;
if (i < n-1) {
printf("+") ;
for (j=0; j<n; j++) {
printf("-") ;
if (j < n-1)
printf("+") ;
}
printf("+\n") ;
}
}

printf("+") ;
for (i=0; i<n; i++) {
printf("-") ;
if (i < n-1)
printf("+") ;
}
printf("+\n\n") ;
}

#define abs(n) ((n)<(0)?(-(n)):(n))

void
place(int r, int n)
{
int i, j ;
if (r == n) {
// We filled in all rows…
total++ ;
print(board, n) ;
} else {
for (i=0; i<n; i++) {
board[r] = i ;
for (j = 0; j<r; j++) {
if (board[j] == board[r])
goto skipit ;
if (abs(board[j]-board[r]) == abs(j-r))
goto skipit ;
}
place(r+1, n) ;
skipit:
continue ;
}
}
}

int
main(int argc, char *argv[])
{
int n = atoi(argv[1]) ;
place(0, n) ;
if (total == 0)
fprintf(stderr, "There are no solutions for the %dx%d board..\n", n, n) ;
else
fprintf(stderr, "There is %d solution%s for the %dx%d board.\n",
total, total > 1 ? "s" : "", n, n) ;
return 0 ;
}
[/sourcecode]

Fun.

A question on Quora set me thinking about solving the N Queens problem, which is to list all ways that N queens can be positioned on an NxN checkerboard such that no queen can attack the other. I seemed to have misplaced my implementation of this that I did in Python, so I decided to do one in C while watching Agents of Shield. The code in general shows the lack of attention, but it does work. It can find all 92 solutions for the 8×8 checkerboard in under one second, but slows down rapidly after that, taking nearly half an hour to find all 73,712 solutions for the 13×13 board.

This program isn’t completely unclever (in fact, I think it is too clever in a way) but it should be properly described as a brute force search, since it generates all N! ways of positioning N queens in different rows, and tests them for diagonals. Thus, it’s runtime is O(N!), which isn’t great. It doesn’t even do backtracking, which would undoubtedly help a great deal.

One good page I found googling this morning is this one by Jeff Somer. His program is much more clever than mine. My estimate is that my program would take well over 100,000 years to count all the positions for a 21×21 board, Jeff’s does it in about a week.

Another cool page is this one, which introduces the idea of “super-queens”, which also capture with the same moves as a knight. Only one unique solution for N=10 exists, which is pretty cool. For higher N, more solutions become possible.

Code is archived here.

[sourcecode lang=”cpp”]
#include <stdio.h>
#include <stdlib.h>

#define MAX_N (15)

int board[MAX_N] ;
int total = 0 ;

void
print(int board[MAX_N], int n)
{
int i, j ;

printf("+") ;
for (i=0; i<n; i++) {
printf("-") ;
if (i < n-1)
printf("+") ;
}
printf("+\n") ;

for (i=0; i<n; i++) {
printf("|") ;
for (j=0; j<n; j++) {
if (j == board[i])
printf("O") ;
else
printf(" ") ;
if (j < n-1)
printf("|") ;
}
printf("?\n") ;
if (i < n-1) {
printf("+") ;
for (j=0; j<n; j++) {
printf("-") ;
if (j < n-1)
printf("+") ;
}
printf("+\n") ;
}
}

printf("+") ;
for (i=0; i<n; i++) {
printf("-") ;
if (i < n-1)
printf("+") ;
}
printf("+\n\n") ;
}

#define abs(n) ((n)<(0)?(-(n)):(n))

void
check(int board[MAX_N], int n)
{
int col[MAX_N] ;
int i, j ;

for (i=n-1; i>=0; i–) {
col[i] = board[i] ;
for (j=i+1; j<n; j++) {
if (col[i] <= col[j])
col[j]++ ;
}
}

// now, check for diagonals..
for (i=0; i<n; i++)
for (j=i+1; j<n; j++)
if (abs(col[i]-col[j]) == abs(j-i))
return ;

// we have a winner…
total++ ;
print(col, n) ;
}

void
place(int i, int n)
{
if (i == n) {
// check board
check(board, n) ;
} else {
int which ;
for (which=0; which < n-i; which++) {
board[i] = which ;
// recurse…
place(i+1, n) ;
}
}
}

int
main(int argc, char *argv[])
{
int n = atoi(argv[1]) ;
place(0, n) ;
if (total == 0)
fprintf(stderr, "There are no solutions for the %dx%d board..\n", n, n) ;
else
fprintf(stderr, "There is %d solution%s for the %dx%d board.\n",
total, total > 1 ? "s" : "", n, n) ;
return 0 ;
}
[/sourcecode]

I was trying to figure out how to screencast to twitch.tv using ffmpeg. A couple of hours of tinkering resulted in the following command line which does a bunch of stuff.

• It captures the X desktop at 15 fps and 1920×1080 resolution.
• It grabs frames from my webcam (a Logitech Pro 9000) at 320×240 resolution.
• It then combines the two into a 1024×576 image, with the video overlayed at the top right and a banner at the bottom that displays a couple of lines of text.
• It then ships it to the twitch.tv server.  If you grab this code, you need to add your own streaming URL for your own channel.

[sourcecode lang=”bash”]
#!/bin/bash

/home/markv/bin/ffmpeg \
-y -thread_queue_size 64 -f x11grab -s 1920×1080 -framerate 15 -i :0.0+0,0 \
-thread_queue_size 64 -f v4l2 -input_format mjpeg -framerate 5 -video_size 320×240 -i /dev/video0 \
-filter_complex \
"[0:v] scale=1024:576, setpts=PTS-STARTPTS [bg]; \
[1:v] setpts=PTS-STARTPTS [fg]; \
color=0x336699cc:1024×64, drawtext=textfile=twitch.txt:fontfile=/usr/share/fonts/truetype/dejavu/DejaVuSansMono-Bold.ttf:x=10:y=16:fontsize=16:fontcolor=white [bottom] ; \
[bg][fg] overlay=W-w-16:16 [out2]; \
[out2][bottom] overlay=0:H-64, format=yuv420p [out]" \
-map "[out]" \
-vsync 1 \
-c:v libx264 -b:v 500k -maxrate 500k -bufsize 1000k -framerate 15 -g 30 -crf 30 -preset fast -pix_fmt yuv420p -tune zerolatency \
-f flv rtmp://live.twitch.tv/app/live_XXXXXXXX_XXXXXXXXXXXXXXXXXXXXXXXXXXXXXX
[/sourcecode]

A few additional notes:

• The default DNS server for my ISP don’t serve DNS requests for the live.twitch.tv server.   I fixed this by adding the Google DNS servers to my router (8.8.8.8 and 8.8.4.4).
• The script appears to work pretty well, but sometimes has difficulty starting up.  And, when the script crashes, the remote clients don’t time out for a considerable time.
• I haven’t tested this extensively.

Buyer beware, but I hope it is useful.

Most of my hacking occurs in a vacuum: where I sit in my living room or in my home office and toil away silently on projects which occasionally get documented here, but which all too often are just my way of passing the time. On the way to work, I was asking myself what I could do to boost my own excitement about these projects, and provide some incentive to do more, and on a more regular basis.

So, I had an idea which is almost certainly not new: the idea of a virtual hackerspace.

For years, I used to donate my Friday evenings to the Chabot Amateur Telescope Makers workshop. I’d go down and spend three or four hours showing up, seeing who needed help on a telescope project, or I’d bring my own and work on that. I want to create a more generic “workshop network”, where people can meet regularly for a kind of hackerspace parallel play using video conferencing technology.

In some sense, it’s just an extension of Google Hangouts. The idea would be that each participant would have a webcam/microphone setup, and at the appointed time, we could all just open our cameras and mics, say “hi” to one another and then go about our business, potentially sharing our projects or asking questions of the group at large. I’ve mostly used Hangouts for simple one-to-one conversations, and have little experience with larger groups, and didn’t really find any obvious links about how to manage larger groups. Does anyone have any recommendations on how to setup such a network? I am not really interested in creating a “show”, but really more of a set of spaces which encourage mutual collaboration and interest.

I’m willing to entertain other technologies as well, if people have better suggestions.

And, if you would be interested in joining in this kind of “network”, drop me a note here or on twitter (@brainwagon). I’ll try to do an update of what I learn.

Okay, it’s been a long time since I wrote anything here. Not really a lot dramatic going on in life, I just have been spending my free time writing for Quora rather than my own blog. But I still am nerding out from time to time. Last night I dusted off an old project of mine and carried it a bit further…

I had written a short post before about a simulator I wrote for Caxton Foster’s “Blue” computer architecture described in his book Computer Architecture. I have the third edition published in 1985. The “Blue” architecture is ridiculously simple: only sixteen instructions, 4096 words of memory, and only one addressing mode. If you click back to my previous post, you’ll see a complete behavioral simulator for it, written in less than an hour.

Somehow this came back up, and I was suddenly intrigued by the idea of trying to write a simple program for it, just to test my ideas about how awful such a machine would be. Ultimately, my goal is to write a simple program that can compute the value of pi to around 100 decimal places. Such a program seems doable, but it’s not a complete cakewalk. But to achieve this, I thought it might be fun to write a simple assembler.

So, I shook the cobwebs that have covered the bits of my brain that understood yacc/lex/bison/flex and wrote a simple assembler for the architecture. It totals only about 250 lines of code, but can handle symbolic labels and all the instructions. It took me about two hours of wall clock time, with my attention split between programming and watching the latest episode of Grimm.

I doubt the assembler is of any real interest, but eventually I’ll get the code onto github.

I then sat down this morning, and wrote this simple program to take the signed value at the memory location VALUE and print it as a signed decimal number. It prints the sign then five digits, with leading zeros if necessary. I didn’t bother to comment
the code, but here it is…

[sourcecode lang=”text”]
PRINTVALUE:
LDA VALUE
JMA NEG
LDA PLUS
OUT
POS:
LDA S0
STA TMP0
SRJ DODIGIT
LDA S1
STA TMP0
SRJ DODIGIT
LDA S2
STA TMP0
SRJ DODIGIT
LDA S3
STA TMP0
SRJ DODIGIT
LDA S4
STA TMP0
SRJ DODIGIT
HLT

DODIGIT:
IOR JMPBIT
STA RETURN
LDA ZERO
STA DIGIT
LOOP: LDA VALUE
ADD TMP0
JMA DONE
STA VALUE
LDA DIGIT
ADD ONE
STA DIGIT
JMP LOOP
DONE:
LDA DIGIT
ADD FE
OUT
RETURN:
JMP 0

NEG:
LDA MINUS
OUT
LDA VALUE
XOR ONES
ADD ONE
STA VALUE
JMP POS

VALUE: .WORD 12323
TMP0: .WORD 0
DIGIT: .WORD 0
S0: .WORD -10000
S1: .WORD -1000
S2: .WORD -100
S3: .WORD -10
S4: .WORD -1
ZERO: .WORD 0
ONE: .WORD 1
ONES: .WORD $FFFF
JMPBIT: .WORD $A000
MINUS: .STRING "-"
PLUS: .STRING "+"
FE: .WORD 48
[/sourcecode]

The assembler spits out a series of 16 bit words which can be loaded into my
simulator…

[sourcecode lang=”text”]
0x602B, 0x9024, 0x6038, 0xC000, 0x602E, 0x702C, 0x8014, 0x602F,
0x702C, 0x8014, 0x6030, 0x702C, 0x8014, 0x6031, 0x702C, 0x8014,
0x6032, 0x702C, 0x8014, 0x0000, 0x4036, 0x7023, 0x6033, 0x702D,
0x602B, 0x102C, 0x9020, 0x702B, 0x602D, 0x1034, 0x702D, 0xA018,
0x602D, 0x1039, 0xC000, 0xA000, 0x6037, 0xC000, 0x602B, 0x2035,
0x1034, 0x702B, 0xA004, 0x3023, 0x0000, 0x0000, 0xD8F0, 0xFC18,
0xFF9C, 0xFFF6, 0xFFFF, 0x0000, 0x0001, 0xFFFF, 0xA000, 0x002D,
0x002B, 0x0030,
[/sourcecode]

The data above gets simply compiled into my simulator and runs.

Okay, so what’s fun to note about this?

There is only a single register, the accumulator. You spend a LOT of time loading things, modifying the value, and storing them back into main memory. There is no “immediate mode”, so you have to create memory locations to store common values like “1” and “0”. DODIGIT is a subroutine, which is called by the SRJ instruction. SRJ puts the PC into the accumulator, and then jumps to the specified address. To “return”, you OR in the bits to the accumulator to form a JMP instruction, and then store that at the end of your subroutine. There is no call stack. Although not demonstrated particularly here, the processor does not implement indexing or indirection. There is also no real condition registers such as CARRY or OVERFLOW, so implementing multi-precision arithmetic might be a challenge.

Foster’s book also details additions to this architecture, eventually becoming INDIGO, an architecture which is rather similar to a PDP-8.

Sure, if you are going to really learn computer archtictures, Patterson and Hennessy is probably a better path, but there is something like of pleasing in this archaic trip down memory lane. My pi computing program will percolate in my brain for a bit, and will find implementation on some other evening.

Addendum: Hackaday recently posted about Al Williams’ FPGA implementation of an architecture which is based upon Foster’s Blue machine. I believe he made a number of changes that make it more practical, but it might be worth looking at. He wrote a monitor, which seems to use opcodes which aren’t compatible with mine.

Addendum²: Pondering it some more throughout the day, it seems difficult to implement my idea of a pi computing program for this virtual machine. All of the algorithms that I can think of require 32 bit numbers, and the Blue architecture simply lacks the capabilities needed to implement it. It also is pretty weak on conditional statements: the only condition that you can branch on is the sign bit of the accumulator.